Question

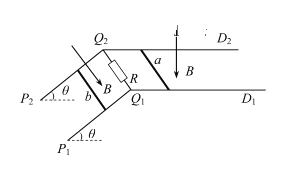
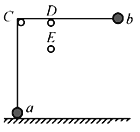
【题目】如图所示，a、b两个小球用一根不可伸长的细线连接，细线绕过固定光滑水平细杆CD，与光滑水平细杆口接触，C、D在同一水平线上。D到小球b的距离是L，在D的正下方也固定有一光滑水平细杆DE。D、E间距为，小球a放在水平地面上，细线水平拉直，由静止释放b，当细线与水平细杆E接触的一瞬间，小球a对地面的压力恰好为0，不计小球大小，则下列说法正确的是

A.细线与水平细杆E接触的一瞬间，小球b加速度大小不变

B.细线与水平细杆E接触的一瞬间，小球b速度发生变化

C.小球a与小球b质量比为5：1

D.将D、E细杆向左平移相同的一小段距离再固定，由静止释放小球b，线与E相碰的一瞬间，小球a会离开地面。

Answer 1

【答案】C

【解析】

AB．细线与水平细杆接触瞬间，小球的速度不会突变，但是由与小球做圆周运动半径变小，由可知，其加速度变大，故A、B错误；

C．当细线与水平细杆E接触的一瞬间，对小球a可知，细线中的拉力为

对小球b，由牛顿第二定律可得

由机械能守恒可得

解得

故C正确；

D．将D、E细杆向左平移相同的一小段距离x，则

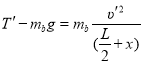
解得

故小球a不会离开地面，故D错误；

故选C。