题目内容
如图所示，用轻滑轮悬挂重力为G的物体．轻绳总长L，绳能承受的最大拉力是2G．现将轻绳一端固定，另一端缓慢向右移动距离d而使绳不断，则d的最大值为
- A.
- B.
- C.
- D.
D
分析：将一端缓慢向右移动，两绳的夹角增大，所受的拉力增大，当绳子的拉力达到最大值2G时，绳子刚要被拉断，距离达到最大值．以滑轮为研究对象，根据平衡条件求得此时两绳之间的夹角，再根据几何关系求得绳子两端之间距离的最大值．
解答：设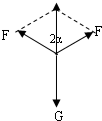
距离达到最大值时，绳子的夹角为2α．此时绳子的拉力达到最大值F=2G．
以滑轮为研究对象，根据平衡条件得：
2Fcosα=G
解得，cosα=
，则sinα=
根据几何知识得：AB之间距离的最大值d=L?2sinα=L
故选D．
点评：本题是平衡条件与几何知识的综合应用，作出力图是解题的基础和关键．
分析：将一端缓慢向右移动，两绳的夹角增大，所受的拉力增大，当绳子的拉力达到最大值2G时，绳子刚要被拉断，距离达到最大值．以滑轮为研究对象，根据平衡条件求得此时两绳之间的夹角，再根据几何关系求得绳子两端之间距离的最大值．
解答：设
距离达到最大值时，绳子的夹角为2α．此时绳子的拉力达到最大值F=2G．以滑轮为研究对象，根据平衡条件得：
2Fcosα=G
解得，cosα=
，则sinα=根据几何知识得：AB之间距离的最大值d=L?2sinα=
L故选D．
点评：本题是平衡条件与几何知识的综合应用，作出力图是解题的基础和关键．
练习册系列答案
相关题目
如图所示，用物块支撑的粗糙斜面顶端安有定滑轮，两质量相等的物块P、Q用轻绳连接并跨过滑轮（不计滑轮的摩擦），P悬于空中，Q放在斜面上，均处于静止状态．当将支撑物块向斜面左端移动一小段距离，使斜面倾角θ增大后，P、Q仍静止不动，则（ ）
（2006?塘沽区模拟）如图所示，表面粗糙的固定斜面顶端安有滑轮，两物块P、Q用轻绳连接并跨过滑轮（不记滑轮的质量和摩擦），P悬于空中，Q放在斜面上，均处于静止状态．当用水平的恒力推Q时，P、Q仍静止不动，则：（ ）
如图所示，用物块支撑的粗糙斜面顶端安有定滑轮，两质量相等的物块P、Q用轻绳连接并跨过滑轮（不计滑轮的摩擦），P悬于空中，Q放在斜面上，均处于静止状态．当将支撑物块向斜面左端移动一小段距离，使斜面倾角θ增大后，P、Q仍静止不动，则
