题目内容
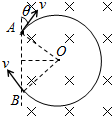如图所示，AB的右侧有方向垂直纸面向里匀强磁场，磁感应强度大小为B，一个带负电的粒子（重力不计）质量为m，电荷量为q，以速率v与AB成θ=30°从A点射入匀强磁场中，求：（1）出射点B到入射点A的距离LAB；
（2）粒子在磁场中运动的时间t．
分析：（1）根据牛顿第二定律，由洛伦兹力提供向心力，从而求出半径，再由几何关系，结合对称性，即可求解；
（2）根据运动的周期公式，结合圆心角，即可求解．
（2）根据运动的周期公式，结合圆心角，即可求解．
解答：解：（1）粒子进入磁场后在洛伦兹力的作用下做匀速圆周运动，洛伦兹力提供向心力，有：qvB=m
解得粒子做圆周运动的半径：r=
因为θ=30°，
根据对称性原则，由几何关系可知△AOB为等边三角形，
所以出射点B到入射点A的距离LAB=r=
（2）粒子在磁场中运动的周期：T=
=
，
所以粒子在磁场中运动的时间：t=
答：（1）出射点B到入射点A的距离LAB=
；
（2）粒子在磁场中运动的时间t=
．
| v2 |
| r |
解得粒子做圆周运动的半径：r=
| mv |
| qB |
因为θ=30°，
根据对称性原则，由几何关系可知△AOB为等边三角形，
所以出射点B到入射点A的距离LAB=r=
| mv |
| qB |
（2）粒子在磁场中运动的周期：T=
| 2πr |
| v |
| 2πm |
| qB |
所以粒子在磁场中运动的时间：t=
| 5πm |
| 3qB |
答：（1）出射点B到入射点A的距离LAB=
| mv |
| qB |
（2）粒子在磁场中运动的时间t=
| 5πm |
| 3qB |
点评：考查粒子在磁场中做匀速圆周运动，掌握牛顿第二定律的应用，理解洛伦兹力提供向心力，并注意运动的时间除与周期有关外，还关注圆弧的圆心角．
练习册系列答案
开心蛙口算题卡系列答案
相关题目
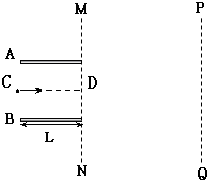如图所示，AB为一对平行板，板间存在匀强电场，板长L=16cm，两板间距离d=16cm，两板间电势差UAB=+1200V．带电粒子的电荷量为q=+1.0×10-10C、质量m=1.0×10-20kg，该粒子沿电场中心线CD以初速度υ0=4×106m/s垂直电场线射入电场．AB板右侧MN、PQ区域存在水平向右的匀强电场，MN与PQ间的电势差为1200V（粒子的重力不计）
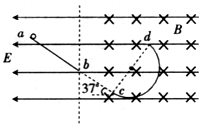（2009?淮南三模）如图所示，ab为与水平面成37°角的倾斜轨道，其延长线在c点与半圆轨道cd相切，cd的半径R=1.2m，全部轨道由绝缘材料制成且位于竖直内面内．整个空间存在水平向左的匀强电场E，ab轨道b端的右侧空间中存在垂直纸面向里的匀强磁场B．-个质量m=0.24kg的带电小球沿ab轨道下滑，至b点时的速度vb=12m/s，接着沿直线bc（此处无轨道）匀速运动到c处进入半圆轨道cd，且到达d点时对轨道的压力大小FN=2.7N，小球从d点飞出时磁场消失．取g=10m/s2，sin37°=0.6，cos37°=0.8，
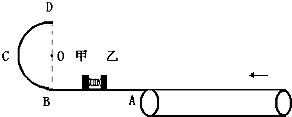如图所示，光滑的水平面AB（足够长）与半径为R=0.8m的光滑竖直半圆轨道BCD在B点相切，D点为半圆轨道最高点．A点的右侧等高地放置着一个长为L=20m、逆时针转动速度为v0=10m/s的传送带．用轻质细线连接甲、乙两物体，中间夹一轻质弹簧，弹簧与甲乙两物体不栓接．甲的质量为m1=3kg，乙的质量为m2=1kg，甲、乙均静止在光滑的水平面上．现固定乙球，烧断细线，甲离开弹簧后进入半圆轨道并可以通过D点，且过D点时对轨道的压力恰好等于甲的重力．传送带与乙物体间摩擦因数为0.6，重力加速度g取l0m/s2，甲、乙两物体可看作质点．