题目内容
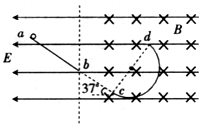 (2009?淮南三模)如图所示,ab为与水平面成37°角的倾斜轨道,其延长线在c点与半圆轨道cd相切,cd的半径R=1.2m,全部轨道由绝缘材料制成且位于竖直内面内.整个空间存在水平向左的匀强电场E,ab轨道b端的右侧空间中存在垂直纸面向里的匀强磁场B.-个质量m=0.24kg的带电小球沿ab轨道下滑,至b点时的速度vb=12m/s,接着沿直线bc(此处无轨道)匀速运动到c处进入半圆轨道cd,且到达d点时对轨道的压力大小FN=2.7N,小球从d点飞出时磁场消失.取g=10m/s2,sin37°=0.6,cos37°=0.8,
(2009?淮南三模)如图所示,ab为与水平面成37°角的倾斜轨道,其延长线在c点与半圆轨道cd相切,cd的半径R=1.2m,全部轨道由绝缘材料制成且位于竖直内面内.整个空间存在水平向左的匀强电场E,ab轨道b端的右侧空间中存在垂直纸面向里的匀强磁场B.-个质量m=0.24kg的带电小球沿ab轨道下滑,至b点时的速度vb=12m/s,接着沿直线bc(此处无轨道)匀速运动到c处进入半圆轨道cd,且到达d点时对轨道的压力大小FN=2.7N,小球从d点飞出时磁场消失.取g=10m/s2,sin37°=0.6,cos37°=0.8,| 15 |
(1)小球所带电荷的种类.
(2)小球离开d点后的运动轨迹与直线ac的交点距c点的距离.
(3)小球在半圆轨道上运动时克服摩擦力所做的功.
分析:带电粒子在只有电场的倾斜轨道上做匀加速运动后,进入电场与磁场混合的场中做匀速直线运动,重力、洛伦兹力与电场力处于平衡状态,接着沿半圆轨道运动刚好能达到D点,最后从D点做类平抛运动,此时所受到的合力正好与速度相互垂直.因此由电场力与电场强度方向可确定小球所带电性,同时利用平抛运动规律可得小球垂直与速度方向上发生的位移,从而求出运动的时间,最终确定沿速度方向的运动的位移.小球在半圆轨道上由运动定理可得克服摩擦力做功多少.
解答: 解:(1)由电场力与电场强度方向可确定小球所带正电荷;
解:(1)由电场力与电场强度方向可确定小球所带正电荷;
(2)依题意可知:小球在BC间做匀速直线运动.
在C点的速度为:vc=vB=
m/s,在BC段其受力如图所示,
设重力和电场力合力为F.
F=qvCB
又 F=
=
=3N
解得:qB=
=
在D处由牛顿第二定律可得:qBvD+F=
将 qB=
代入上式并化简得:4vD2-5vD-114=0
解得:vD=6m/s,vD=
m/s(舍去)
小球离开D点后作类平抛运动,其加速度为:a=
=
m/s2
由2R=
at2
代入数据得:t=0.62s
s=vDt=6×0.62=3.7m
(3)CD段克服摩擦力做功Wf
由动能定理可得:-Wf-2FR=
m(vD2-vC2)
代入数据,解得:Wf=5.76J
答:(1)小球带正电荷.
(2)小球离开d点后的运动轨迹与直线ac的交点距c点的距离为3.7m.
(3)小球在半圆轨道上运动时克服摩擦力所做的功为5.76J.
 解:(1)由电场力与电场强度方向可确定小球所带正电荷;
解:(1)由电场力与电场强度方向可确定小球所带正电荷;(2)依题意可知:小球在BC间做匀速直线运动.
在C点的速度为:vc=vB=
| 100 |
| 7 |
设重力和电场力合力为F.
F=qvCB
又 F=
| mg |
| cos37° |
| 0.24×10 |
| 0.8 |
解得:qB=
| F |
| vc |
| 1 |
| 4 |
在D处由牛顿第二定律可得:qBvD+F=
| mvD2 |
| R |
将 qB=
| 1 |
| 4 |
解得:vD=6m/s,vD=
| 19 |
| 4 |
小球离开D点后作类平抛运动,其加速度为:a=
| F |
| m |
| 25 |
| 2 |
由2R=
| 1 |
| 2 |
代入数据得:t=0.62s
s=vDt=6×0.62=3.7m
(3)CD段克服摩擦力做功Wf
由动能定理可得:-Wf-2FR=
| 1 |
| 2 |
代入数据,解得:Wf=5.76J
答:(1)小球带正电荷.
(2)小球离开d点后的运动轨迹与直线ac的交点距c点的距离为3.7m.
(3)小球在半圆轨道上运动时克服摩擦力所做的功为5.76J.
点评:小球从D点飞出后,正好受到重力与电场力且这两个力的合力与速度垂直,所以刚好做类平抛运动.因此可以将倾斜轨道等效看成水平面,相当于小球做平抛运动,从而可以运用平抛运动规律来处理.

练习册系列答案
相关题目
 (2009?淮南三模)在竖直平面内,有根光滑金属杆弯成如图所示形状,相应的曲线方程为y=Acosx,将一个光滑小环套在该金属杆上,并从x=0、y=A处以某一初速度沿杆向+x方向运动.运动过程中( )
(2009?淮南三模)在竖直平面内,有根光滑金属杆弯成如图所示形状,相应的曲线方程为y=Acosx,将一个光滑小环套在该金属杆上,并从x=0、y=A处以某一初速度沿杆向+x方向运动.运动过程中( )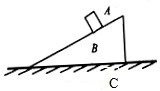 (2009?淮南三模)如图所示,物块A沿楔形块B的斜面下滑时,B相对于水平地面C静止不动,设A、B间的动摩擦因数为μ1,B、C间的动摩擦因数为μ2,则下列说法中不可能的是( )
(2009?淮南三模)如图所示,物块A沿楔形块B的斜面下滑时,B相对于水平地面C静止不动,设A、B间的动摩擦因数为μ1,B、C间的动摩擦因数为μ2,则下列说法中不可能的是( )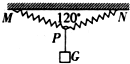 (2009?淮南三模)如图所示,原长为l、劲度系数为k的轻弹簧固定于同一高度的M、N两点,在弹簧的中点P处悬挂一重为G的物体,整个装置处于平衡,此时MP与PN之间的夹角为120°,则此时弹簧的总长度为( )
(2009?淮南三模)如图所示,原长为l、劲度系数为k的轻弹簧固定于同一高度的M、N两点,在弹簧的中点P处悬挂一重为G的物体,整个装置处于平衡,此时MP与PN之间的夹角为120°,则此时弹簧的总长度为( )