题目内容
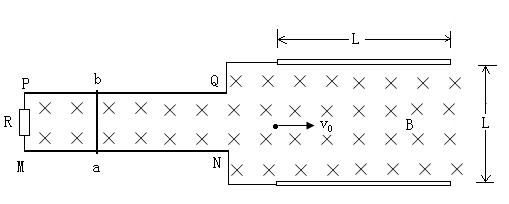
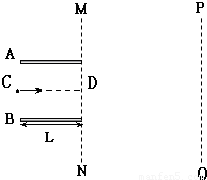
 如图所示,AB为一对平行板,板间存在匀强电场,板长L=16cm,两板间距离d=16cm,两板间电势差UAB=+1200V.带电粒子的电荷量为q=+1.0×10-10C、质量m=1.0×10-20kg,该粒子沿电场中心线CD以初速度υ0=4×106m/s垂直电场线射入电场.AB板右侧MN、PQ区域存在水平向右的匀强电场,MN与PQ间的电势差为1200V(粒子的重力不计)
如图所示,AB为一对平行板,板间存在匀强电场,板长L=16cm,两板间距离d=16cm,两板间电势差UAB=+1200V.带电粒子的电荷量为q=+1.0×10-10C、质量m=1.0×10-20kg,该粒子沿电场中心线CD以初速度υ0=4×106m/s垂直电场线射入电场.AB板右侧MN、PQ区域存在水平向右的匀强电场,MN与PQ间的电势差为1200V(粒子的重力不计)(1)求粒子从AB间匀强电场射出时速度的方向及大小.
(2)求粒子射出PQ时的动能.
分析:(1)粒子沿电场中心线CD以初速度υ0=4×106m/s垂直电场线射入电场,做类平抛运动,由运动的分解法可知:水平方向做匀速直线运动,竖直方向做匀加速运动,由牛顿第二定律 运动学公式结合求解粒子离开AB板间电场时竖直方向的分速度vy,粒子从AB间匀强电场射出时速度的大小v=
,tanα=
,求出速度v与水平方向的夹角.
(2)粒子MN与PQ间的电场中,电场力做功为qU,根据动能定理求解粒子射出PQ时的动能.
|
| vy |
| v0 |
(2)粒子MN与PQ间的电场中,电场力做功为qU,根据动能定理求解粒子射出PQ时的动能.
解答:解:(1)粒子在平行板AB间运动时做类平抛运动,则有
水平方向:L=v0t,
竖直方向:vy=at,a=
=
解得 vy=
则粒子从AB间匀强电场射出时速度大小为 v=
=
代入解得,v=5×106m/s
设速度方向与水平方向夹角为α,则tanα=
=
代入解得,tanα=
,得α=37°.
(2)粒子MN与PQ间的电场中运动时,根据动能定理得
qUAB=Ek-
mv2
解得,Ek=1.25×10-8J.
答:(1)粒子从AB间匀强电场射出时速度大小为5×106m/s,方向与水平成37°;
(2)粒子射出PQ时的动能是1.25×10-8J.
水平方向:L=v0t,
竖直方向:vy=at,a=
| qE |
| m |
| qUAB |
| md |
解得 vy=
| qUABL |
| mdv0 |
则粒子从AB间匀强电场射出时速度大小为 v=
|
|
代入解得,v=5×106m/s
设速度方向与水平方向夹角为α,则tanα=
| vy |
| v0 |
| qUABL | ||
md
|
代入解得,tanα=
| 3 |
| 4 |
(2)粒子MN与PQ间的电场中运动时,根据动能定理得
qUAB=Ek-
| 1 |
| 2 |
解得,Ek=1.25×10-8J.
答:(1)粒子从AB间匀强电场射出时速度大小为5×106m/s,方向与水平成37°;
(2)粒子射出PQ时的动能是1.25×10-8J.
点评:本题是常规题,运用运动的分解法研究粒子的类平抛运动,根据动能定理求解动能,都是常用的方法.

练习册系列答案
 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
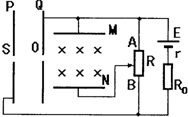 (2003?顺德区模拟)如图所示,相距为d的水平金属板M、N在左侧有一对竖直金属板P、Q,板P上的小孔S正对极Q上的小孔O,M、N间有垂直纸面向里的匀强磁场,在小孔S处有一带负电粒子,其重力和初速均不计,当变阻器的滑动触头在AB的中点时,带负电粒子恰能在M、N间做直线运动,当滑动变阻器滑片滑到A点后,( )
(2003?顺德区模拟)如图所示,相距为d的水平金属板M、N在左侧有一对竖直金属板P、Q,板P上的小孔S正对极Q上的小孔O,M、N间有垂直纸面向里的匀强磁场,在小孔S处有一带负电粒子,其重力和初速均不计,当变阻器的滑动触头在AB的中点时,带负电粒子恰能在M、N间做直线运动,当滑动变阻器滑片滑到A点后,( )