题目内容
 如图所示,宇航员站在某质量分布均匀的星球表面一斜坡上P点,沿水平方向以初速度v0抛出一个小球,测得小球经时间t落到斜坡上另一点Q,斜面的倾角为α,已知该星球的半径为R,万有引力常量为G.求该星球的密度.
如图所示,宇航员站在某质量分布均匀的星球表面一斜坡上P点,沿水平方向以初速度v0抛出一个小球,测得小球经时间t落到斜坡上另一点Q,斜面的倾角为α,已知该星球的半径为R,万有引力常量为G.求该星球的密度.分析:根据平抛运动规律列出水平方向和竖直方向的位移等式,结合几何关系求出重力加速度.
忽略地球自转的影响,根据万有引力等于重力列出等式.
根据密度公式求解.
忽略地球自转的影响,根据万有引力等于重力列出等式.
根据密度公式求解.
解答:解:设该星球表现的重力加速度为g,根据平抛运动规律:
水平方向:x=v0t
竖直方向:y=
gt2
平抛位移与水平方向的夹角的正切值tanα=
=
得g=
设该星球质量M,对该星球表现质量为m1的物体有
=m1g
M=
由V=
πR3
得ρ=
=
答:该星球的密度是
.
水平方向:x=v0t
竖直方向:y=
| 1 |
| 2 |
平抛位移与水平方向的夹角的正切值tanα=
| y |
| x |
| ||
| v0t |
得g=
| 2v0tanα |
| t |
设该星球质量M,对该星球表现质量为m1的物体有
| GMm1 |
| R2 |
M=
| gR2 |
| G |
| 4 |
| 3 |
得ρ=
| M |
| V |
| 3v0tanα |
| 2RGtπ |
答:该星球的密度是
| 3v0tanα |
| 2RGtπ |
点评:处理平抛运动的思路就是分解.
重力加速度g是天体运动研究和天体表面宏观物体运动研究联系的物理量.
重力加速度g是天体运动研究和天体表面宏观物体运动研究联系的物理量.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
 如图所示,宇航员站在某质量分布均匀的星球表面一斜坡上的P点沿水平方向以初速度υ0抛出一个小球,测得小球经时间t落到斜坡上另一点Q,斜面的倾角为θ,已知该星球半径为R,万有引力常量为G,求:
如图所示,宇航员站在某质量分布均匀的星球表面一斜坡上的P点沿水平方向以初速度υ0抛出一个小球,测得小球经时间t落到斜坡上另一点Q,斜面的倾角为θ,已知该星球半径为R,万有引力常量为G,求: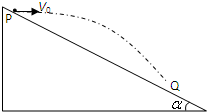 如图所示,宇航员站在某质量分布均匀的星球表面一斜坡上P点沿水平方向以初速度v0抛出一个小球,测得小球经时间t落到斜坡上另一点Q,斜面倾角为α,已知星球半径为R,万有引力常量为G,求:
如图所示,宇航员站在某质量分布均匀的星球表面一斜坡上P点沿水平方向以初速度v0抛出一个小球,测得小球经时间t落到斜坡上另一点Q,斜面倾角为α,已知星球半径为R,万有引力常量为G,求: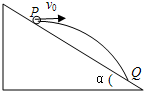 如图所示,宇航员站在某质量分布均匀的星球表面一斜坡上P点,沿水平方向以初速度v0抛出一个小球,测得小球经时间t落到斜坡上另一点Q,斜面的倾角为α,已知该星球的半径为R,万有引力常量为G.则
如图所示,宇航员站在某质量分布均匀的星球表面一斜坡上P点,沿水平方向以初速度v0抛出一个小球,测得小球经时间t落到斜坡上另一点Q,斜面的倾角为α,已知该星球的半径为R,万有引力常量为G.则