题目内容
【题目】如图所示,A,B两个物体放在旋转圆台上,动摩擦因数均为μ,最大静摩擦力数值认为等于滑动摩擦力值.A物体质量为2m,B物体质量为m,A离转轴距离为R,B离轴距离为2R,则当圆台旋转时(设A,B两物都没发生滑动)( )

A. A物体的向心加速度较大
B. B物体所受摩擦力大小一定为μmg
C. 两物体所受摩擦力都相等
D. 当圆台转速增加时,B比A先发生滑动
【答案】CD
【解析】两个物体都做匀速圆周运动,(任意一个)物体受力如图所示:
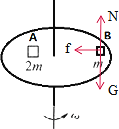
由于两物体共轴转动,它们的角速度ω相等,由题意可知,rB=2rA=2R;A、由a=ω2r可知,则B的向心加速度较大,故A错误;B、B物体做圆周运动的向心力由静摩擦力提供,f=mω2r,可能小于μmg,也可能等于μmg,故B错误;C、两物体做圆周运动的向心力由摩擦力提供,摩擦力的方向与速度方向垂直,摩擦力不做功,fA=(2m)ω2rA=2mω2R,fB=mω2rB=mω2(2R)=2mω2R,则fA=fB,故C正确;D、当摩擦力达到最大静摩擦力时,物体开始滑动,由牛顿第二定律得:μmg=mω2r,解得![]() ,μ相同,轨道半径越大,临界角速度越小,物体越先滑动,因此B比A先滑动,故D正确;故选CD。
,μ相同,轨道半径越大,临界角速度越小,物体越先滑动,因此B比A先滑动,故D正确;故选CD。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目