��Ŀ����
����Ŀ����ͼ��ʾ������Ϊ�ʵ�������A��B�������ֱ�Ϊm��2m��A����һ���Ϊ30�㲢�̶���ˮƽ���ϵĹ⻬б���ϣ�һ�����쳤��������������⻬���ʶ����֣����˷ֱ���A��B�����ӡ���סBʹ����鴦�ھ�ֹ״̬����ʱB�����߶�Ϊh�������պ�������A�ͻ��ּ��������б��ƽ�С��ֽ�B�Ӿ�ֹ�ͷţ�б���㹻�����������ٶ�Ϊg����
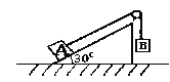
��1��B���ǰ���������Ĵ�СT��
��2������������A��б�������˶���������L��
���𰸡���1��T=mg��2��L=2h
����������1����B���ǰ�������ٶȴ�СΪa������A��ȡ��б������Ϊ��������B��ȡ��ֱ����Ϊ������ţ�ٵڶ����ɵã�T-mgsin30��=ma
2mg-T=2ma
��ã�a��![]() g��T=mg��
g��T=mg��
��2����B���ǰ˲��A���ٶ�Ϊv�����˶�ѧ��ʽ�ã�v2=2ah
��B��غ�A��б�������˶��Ĺ����м��ٶ�Ϊa1����a1=gsin30��
��B��غ�A��б�������˶���������ΪS�����˶�ѧ��ʽ�ã�
-v2=2a1S
S=![]() vt2
vt2
��ã�S=h
����������A��б�������˶���������L=2h��

����Ŀ��ijͬѧ����һ��̽�������͵����쳤�Ĺ�ϵ�����ⵯ�ɵľ���ϵ��k.�������Ƚ����ⵯ�ɵ�һ�˹̶�������̨�ϣ�Ȼ����С�̶��Ǻ��Ŀ̶ȳ���ֱ���ڵ���һ�࣬��ʹ������һ�˵�ָ��ǡ�����ڿ̶ȳ��ϣ���������Ȼ�´�ʱ��ָ��ָʾ�Ŀ̶���ֵ����L0�������¶˹�һ��50 g������ʱ��ָ��ָʾ�Ŀ̶���ֵ����L1�������¶˹�����50 g������ʱ��ָ��ָʾ�Ŀ̶���ֵ����L2���������߸�50 g������ʱ��ָ��ָʾ�Ŀ̶���ֵ����L7.
(1)�±���¼���Ǹ�ͬѧ�Ѳ����6��ֵ��������������ֵ�ڼ�¼ʱ�������ǵĴ������ŷֱ���________��________��
������¼����
�������� | L0 | L1 | L2 | L3 | L4 | L5 | L6 | L7 |
| 1.70 | 3.40 | 5.10 | 8.60 | 10.3 | 12.1 |
(2)ʵ���У�L3��L7����ֵ��û�вⶨ�����������ͼ������������ֵ�����¼���У�
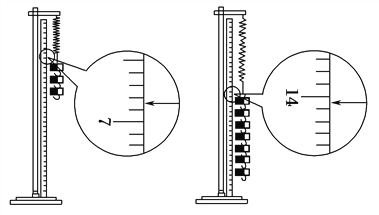
(3)Ϊ������ò������ݣ���ͬѧ������õ���ֵ�����·�����һ���ֱ�������������ֵ��d1��L4��L0��6.90 cm��d2��L5��L1��6.90 cm��d3��L6��L2��7.00 cm.
����������ĸ���ֵ��d4��________��________cm.
(4)�������ϲ�ֵ���������ÿ����50 g����ĵ���ƽ���쳤����L.��L��d1��d2��d3��d4��ʾ��ʽ��Ϊ��L��________���������ݽ����L��________cm.
(5)���㵯�ɵľ���ϵ��k��________N/m.(gȡ9.8 N/kg)