题目内容
【题目】固定在水平面内的两条平行光滑金属导轨，间距L＝0.6m，左端连接一阻值R＝2.0Ω的定值电阻，导轨所在空间存在竖直向上的匀强磁场，磁感应强度B＝1.0T，其俯视图如图所示。长度恰好等于导轨间距的导体棒MN放在导轨上，其质量m＝0.6kg、电阻r＝1.0Ω，与导轨始终垂直且接触良好，导轨的电阻可忽略不计。现用平行于导轨的拉力F作用在导体棒上，使其沿导轨向右匀速运动，速度v0＝5m/s。
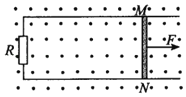
（1）求匀速运动过程中MN两点的电势差，并且指出M、N两点哪点电势高；
（2）某时刻撤去外力F，求撤去外力F后至速度变为v1＝2.0m/s的过程中
a．电流流过外电阻R产生的焦耳热；
b．导体棒MN向右移动的距离。
（3）在上述情景中，金属棒MN相当于一个电源，这时的非静电力与棒中自由电子所受洛伦兹力有关。请根据电动势的定义，推导金属棒MN中的感应电动势E＝BLV。
【答案】（1）2V，N点电势高；（2）a．4.2J；b.15m。（3）棒向右运动时，电子具有向右的分速度，受到沿棒向上的洛伦兹力为：f＝evB,电子在f的作用下，电子从M移动到N的过程中，非静电力做功为：W＝evBL根据电动势定义为：
，解得：E＝Blv；
【解析】
（1）切割磁感应线产生的感应电动势E＝BLv0＝1×0.6×5V＝3V
MN两端的电势差大小
根据右手定则可知，N端为电源的正极，所以N点电势高；
（2）a、根据能量守恒可得回路产生的焦耳热
，
解得：Q＝6.3J
另有 
；
b、设导体棒移动的距离为x，所用时间为t，据动量定理得
，
化简得﹣BLq＝mv1﹣mv0，
据电磁感应的电荷量推论公式
，
联立解得：x＝15m；
（3）棒向右运动时，电子具有向右的分速度，受到沿棒向上的洛伦兹力为：f＝evB
电子在f的作用下，电子从M移动到N的过程中，非静电力做功为：W＝evBL
根据电动势定义为：
解得：E＝Blv
