题目内容
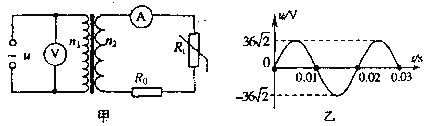
【题目】光滑平行的金属导轨MN和PQ,间距L=1.0m,与水平面之间的夹角α=30°,匀强磁场磁感应强度B=2.0T,垂直与导轨平面向上,MP间接有阻值R=2.0Ω的电阻,其它电阻不计,质量m=2.0kg的金属杆ab垂直导轨放置,如图(a)所示.用恒力F沿导轨平面向上拉金属杆ab,由静止开始运动,v-t图象如图(b)所示.g=10m/s2,导轨足够长.求:

(1)恒力F的大小;
(2)金属杆速度为2.0m/s时的加速度大小;
(3)根据v-t图象估算在前0.8s内电阻上产生的热量(已知在前0.8s内杆的位移为1.12m).
【答案】(1)18N(2)2.0m/s2(3)4.12J
【解析】试题分析:由乙图看出,杆的最大速度为4m/s时,杆做匀速直线运动,根据平衡条件可求出F;金属杆速度为2.0m/s时,求出安培力大小,由牛顿第二定律求解加速度大小;根据速度图象的“面积”大小等于位移,估算出前0.8s内杆的位移,估算时大于等于半格算一个,小于半格舍去.根据能的转化与守恒定律求解电阻R上产生的热量。
(1)对金属杆受力分析如图所示:
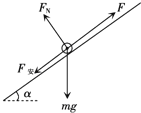
v-t图像可知导轨最后匀速运动且vmax=4m/s
沿斜面方向: ![]() ,
,
安培力为: ![]()
电流为: ![]()
联立并带入数据解得: ![]()
(2)对金属杆由牛顿第二定律可得: ![]()
代入数据解得: ![]()
(3)设在前0.5s内电阻上产生的热量为Q,
则由功能关系可得: ![]()
由v-t图像可知0.8s时速度为:v=2.2m/s,
代入数据解得: ![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目