题目内容
【题目】如图,直角三角形ABC为一棱镜的横截面,∠B=90°,∠C=30°。AC边长为3a,P、Q两点分别位于AC、AB边上,且与A点的距离均为a。平行于BC边的单色细光束从P点射入棱镜,正好从Q点射出,求:
(i)棱镜的折射率;
(ii)若将该光束平移到AC边上与C点距离为a的R点入射,已知光在真空中的传播速度为c,求从R点入射的光束通过棱镜的时间。

【答案】(i)![]() ;(ii)
;(ii)![]()
【解析】
(i)由题意,从P点射入棱镜的光线,其折射光线如图所示,由图可知:
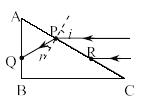
入射角:i=90°-∠C=90°-30°=60°
折射角:r=90°-∠APQ=90°-60°=30°
由折射定律得
![]()
(ii)设该棱镜介质的临界角为C,由临界角公式得:
![]()
从R点射入棱镜的光线,其折射光线如图所示,其入射角、折射角与P点的入射光线相同,图中光线在S点的入射角为θ,由几何知识可知
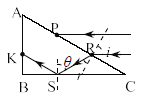
θ=60°>C
光线在S点发生全反射,从AB边上的K点射出
由几何知识可知△SRC为等腰三角形,△KBS∽△ABC
![]()
![]()
设光在棱镜中的传播速度为v,则
![]()
光通过棱镜的时间:
![]()
联立解得
![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目