题目内容
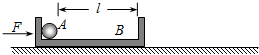
如图所示,A、B两物体叠放在一起以v0的速度沿光滑的水平轨道匀速运动,与静止在同一光滑水平轨道上的木板C发生碰撞,碰撞后B、C以相同的速度运动(不粘合),A滑上C后最终停在木板C的最右端,已知A、B、C质量均相等,A可看成质点,B、C的上表面相平,且B的上表面光滑,木板C长为L.
求:①A物体的最终速度;
②从A滑上木板C到A最终停在木板C最右端所经历的时间.

求:①A物体的最终速度;
②从A滑上木板C到A最终停在木板C最右端所经历的时间.

①B、C碰撞过程动量守恒,以B的初速度方向为正方向,
由动量守恒定律得:mv0=(m+m)v,
A滑上C到A、C相对静止过程,A、C系统动量守恒,以A的初速度方向为正方向,
由动量守恒定律得:mv0+mv=(m+m)v′,
解得:v=
,v′=
v0;
②A、C相互作用过程中,由能量守恒定律得:
fL=
mv02+
mv2-
(m+m)v′2,
以向右为正方向,对A,由动量定理得:
-ft=mv′-mv0,解得:t=
;
答:①A物体的最终速度为
v0;
②从A滑上木板C到A最终停在木板C最右端所经历的时间为
.
由动量守恒定律得:mv0=(m+m)v,
A滑上C到A、C相对静止过程,A、C系统动量守恒,以A的初速度方向为正方向,
由动量守恒定律得:mv0+mv=(m+m)v′,
解得:v=
| v0 |
| 2 |
| 3 |
| 4 |
②A、C相互作用过程中,由能量守恒定律得:
fL=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
以向右为正方向,对A,由动量定理得:
-ft=mv′-mv0,解得:t=
| 4L |
| v0 |
答:①A物体的最终速度为
| 3 |
| 4 |
②从A滑上木板C到A最终停在木板C最右端所经历的时间为
| 4L |
| v0 |

练习册系列答案
相关题目
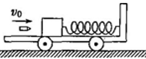

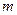 的子弹,以水平速度击中木块,木块滑行距离
的子弹,以水平速度击中木块,木块滑行距离 后,子弹与木块以共同速度运动,子弹射入木块的深度为
后,子弹与木块以共同速度运动,子弹射入木块的深度为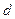 。为表示该过程,甲、乙两同学分别画出了如下图所示的示意图,以下判断中正确的是
。为表示该过程,甲、乙两同学分别画出了如下图所示的示意图,以下判断中正确的是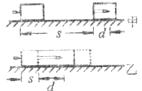
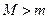 时,甲图正确,当
时,甲图正确,当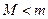 时乙图正确
时乙图正确