题目内容
20.水平光滑且绝缘的桌面上,在相距h=2m的区域间,有如图所示的周期性分布的匀强磁场,磁场区域足够大,每个小磁场区域宽度均为d=1m,磁感应强度B=0.5T,方向如图.正方形闭合导线框边长l=1m,电阻R=2Ω.,质量m=0.lkg;开始时,线框处于图示位置.
(1)从图示位置开始,用外力拉动线框,使它以v=2m/s的速度匀逮向右运动经过磁场区域,求经过t=2s,外力做的功;
(2)从图示位置开始,使整个磁场以v0=2m/s的速度向左匀速运动,求:
①线框速度v=1m/s时的加速度大小;
②最终线框相对于磁场区域移动的距离.
分析 (1)线框匀速运动,左右两个边一直做切割磁感线运动,根据右手定则判断电流方向,根据左手定则判断安培力方向,得到安培力一直向左;根据切割公式求解感应电动势,根据欧姆定律求解感应电流,根据安培力公式求解安培力,根据平衡条件得到拉力大小,根据W=Fx求解拉力功;
(2)①使整个磁场以v0=2m/s的速度向左匀速运动,线框相对磁场的初速度为向右,大小为2m/s,根据切割公式求解感应电动势大小,根据欧姆定律和安培力公式求解安培力大小,根据牛顿第二定律列式求解加速度大小;
②导线框水平方向受安培力,做减速运动,采用微元法,根据牛顿第二定律列式,根据切割公式、欧姆定律和安培力公式表示安培力,根据a=$\frac{△v}{△t}$表示加速度,然后求和即可.
解答 解:(1)线框在不同位置时切割磁感线产生的电动势大小相等,故:E=2Blv,
电流方向不同,但是大小相等,故:I=$\frac{E}{R}$,
线框匀速运动,2s内拉力做的功与安培力做功相等,转化为焦耳热:Q=I2Rt,
解得:Q=4J;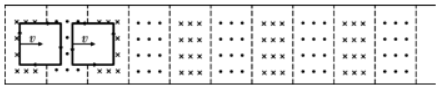
(2)①当线框速度v=1m/s时,切割磁感线的电动势:E=2Bl(v0-v),
电流:I=$\frac{E}{R}$,
安培力与相对运动的方向相反,故:F安=2BIl,
加速度:a=$\frac{{F}_{安}}{m}$,
解得:a=5m/s2;
②最终当线框速度与磁场相等时线框磁通量不再变化,最后匀速运动,
当线框在磁场中运动时,有:E=2Bl(v0-v),I=$\frac{E}{R}$,
${F_安}={B_左}Il+{B_右}Il=\frac{{4{B^2}{l^2}({v_0}-v)}}{R}$,
F安=ma,
可得:$\frac{{4{B^2}{l^2}({v_0}-v)}}{R}=m\frac{△v}{△t}$,
$\sum\frac{{4{B^2}{l^2}{v_{相对}}}}{R}△t=m{v_0}$△t,
$\frac{{4{B^2}{l^2}{x_{相对}}}}{R}=m{v_0}$,
解得:x相对=0.4m;
答:(1)经过t=2s,外力做的功为4J;
(2)①线框速度v=1m/s时的加速度大小为5m/s2;
②最终线框相对于磁场区域移动的距离为4m.
点评 本题是滑轨问题的创新,研究对象变为了导线框,而且磁场是周期性变化的,要明确相对运动,关键是结合切割公式、欧姆定律、安培力公式列式,第二问要采用微元法解题,难度较大.

 阅读快车系列答案
阅读快车系列答案| A. | 观察者静止,火车向他驶来 | |
| B. | 观察者静止,火车离他驶去 | |
| C. | 火车静止,观察者乘汽车向着火车运动 | |
| D. | 火车静止,观察者乘汽车远离火车运动 |
| A. | γ射线是电磁波,它的穿透能力最弱 | |
| B. | γ射线一般伴随着α或β射线产生,它的穿透能力最强 | |
| C. | α射线是原子核自发放射出的氦核流,它的穿透能力最强 | |
| D. | β射线是原子核外电子电离形成的电子流,它具有中等的穿透能力 |
 如图所示,横截面为直角三角形的斜劈P,靠在粗糙的竖直墙面上,力F通过球心水平作用在光滑球Q上,系统处于静止状态.当力F增大时,系统仍保持静止,下列说法正确的是( )
如图所示,横截面为直角三角形的斜劈P,靠在粗糙的竖直墙面上,力F通过球心水平作用在光滑球Q上,系统处于静止状态.当力F增大时,系统仍保持静止,下列说法正确的是( )| A. | 斜劈P所受合外力增大 | B. | 球Q对地面的压力不变 | ||
| C. | 墙面对斜劈P的摩擦力增大 | D. | 斜劈P对竖直墙壁的压力增大 |
 如图所示,水平线MN上方存在匀强磁场,磁感应强度大小为B,方向垂直于纸面向外,MN上方有一单匝矩形异线框abcd,其质量为m,电阻为R,ab边长为L1,bc边长为L2,cd边离MN的高度为h.现将线框由静止释放,线框下落过程中ab边始终保持水平,且ab边离开磁场前已做匀速直线运动,不考虑空气阻力的影响,则从线框静止释放到完全离开磁场的过程中( )
如图所示,水平线MN上方存在匀强磁场,磁感应强度大小为B,方向垂直于纸面向外,MN上方有一单匝矩形异线框abcd,其质量为m,电阻为R,ab边长为L1,bc边长为L2,cd边离MN的高度为h.现将线框由静止释放,线框下落过程中ab边始终保持水平,且ab边离开磁场前已做匀速直线运动,不考虑空气阻力的影响,则从线框静止释放到完全离开磁场的过程中( )| A. | 回路中电流最大值一定为$\frac{B{L}_{1}\sqrt{2gh}}{R}$ | |
| B. | 匀速运动时回路中电流的热功率为$\frac{{m}^{2}{g}^{2}R}{{B}^{2}{{L}_{1}}^{2}}$ | |
| C. | 整个过程中通过导线横截面的电荷量为$\frac{B{L}_{1}{L}_{2}}{R}$ | |
| D. | 整个过程中导线框中产生的热量为mg(h+L2)-$\frac{{m}^{3}{g}^{2}{R}^{2}}{{B}^{4}{{L}_{1}}^{4}}$ |
| A. | 中子与质子结合成氘核的过程中需要吸收能量 | |
| B. | 一束光照射到某种金属上不能发生光电效应,是因为这束光的光强太小 | |
| C. | 依据玻尔理论,氢原子从低能级向高能级跃迁时,电子的动能将减小 | |
| D. | β衰变中产生的β射线实际上是原子的核外电子挣脱原子核的束缚而形成的 |
 某电场中的电场线分布如图所示,现将一带负电的点电荷从A点移至B点需克服电场力做功,则B、C两点的场强和电势的大小关系是( )
某电场中的电场线分布如图所示,现将一带负电的点电荷从A点移至B点需克服电场力做功,则B、C两点的场强和电势的大小关系是( )| A. | EB>EC;φB<φC | B. | EB<EC;φB<φC | C. | EB>EC;φB>φC | D. | EB<EC;φB>φC |

 如图所示,在一水平圆盘上的A点放一物体,质量为m,A到O的距离为2L,在AO连线(O为圆盘中心)的中点B处放另一个完全相同的物体,现使圆盘绕通过圆心O的竖直轴从静止开始运动,并缓慢加快转速,当转速增加到n0时,两个物体中的一个即将开始滑动.求:
如图所示,在一水平圆盘上的A点放一物体,质量为m,A到O的距离为2L,在AO连线(O为圆盘中心)的中点B处放另一个完全相同的物体,现使圆盘绕通过圆心O的竖直轴从静止开始运动,并缓慢加快转速,当转速增加到n0时,两个物体中的一个即将开始滑动.求: