��Ŀ����
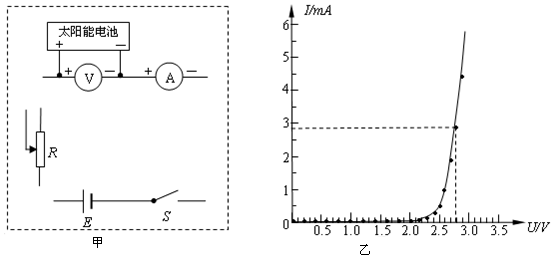
15��ijͬѧ����ͼ��ʾ�ĵ�·�����ⶨ��Դ�綯�ƺ��ڵ��衱��ʵ�飬����ʵ���е�6���ѹU������I�����ݱ�������ֽ�ϣ�
��1���Ը�����Щ���ݵ�������ֽ�ϻ���U-Iͼ�ߣ�
��2������ͼ�������صĵ綯��E=1.50V������r=0.83����
��3���ô˵�·����ĵ綯�Ʊȵ綯�Ƶ���ʵֵƫС�����ƫ��ƫС������ȡ�����
��4������ʵ������û�е�ѹ������������1mA������r1=200���ĵ�����A�͵�����R��װ������Ϊ2V�ĵ�ѹ�����������R��ֵӦ��Ϊ1800����
���� ��1��������㷨�ɵó���Ӧ��ͼ��
��2���ɱպϵ�·ŷķ���ɽ��з��������ͼ������ʼ�����õ綯�ƺ��ڵ��裻
��3������ʵ��ԭ������ʵ���е���
��4�����ݴ�������·�Ĺ��ɽ��з������Ӷ����Ӧ�����ĵ��裮
���  �⣺��1����������ĵ�����ֱ�߽�������ϣ���ͼ��ʾ��
�⣺��1����������ĵ�����ֱ�߽�������ϣ���ͼ��ʾ��
��2�����ݱպϵ�·ŷķ���ɿ�֪��U=E-Ir��
����ͼ��֪����Դ�ĵ綯��Ϊ��E=1.50V��
ͼ���б�ʱ�ʾ��Դ�����裬���У�r=$\frac{1.5-1.0}{0.6}$=0.83����
��3�����ӷ��в�����Ե�Դ�ĵ�������ӷ�����Ϊ��ѹ���ķ������ã�ʹ�������������ƫС�����֪��ʵ��ͼ��������ʾ���Ͳ���ͼ��Ӧ��ͼ��ʾ����ͼ��֪���������ƫС��
��4�����ݴ�����·���ɿ�֪������������ֵΪ��R=$\frac{U-{I}_{g}{R}_{g}}{{I}_{g}}$=$\frac{2-1��1{0}^{-3}��200}{1��1{0}^{-3}}$=1800����
�ʴ�Ϊ����1����ͼ��ʾ����2��1.50��0.83����3��ƫС����4��1800��
���� ���⿼������綯�ƺ��ڵ����ʵ�飬Ҫע����ȷʵ��ԭ����֪��ʵ���е�������Ӱ�죬�Ӷ�����ʵ���д��ڵ���������

��ϰ��ϵ�д�
�����Ŀ
5��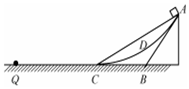 ��ͼ��ʾ��б��AB��AC�ĵ�ͨ��һС��Բ����ˮƽ��������Բ����ADC�ֱ���б��AB��ˮƽ�����У�С����A�˷ֱ��ɾ�ֹ��б��AB��б��AC����ADC�»����Ҷ��ܾ���ˮƽ���ϵ�Q�㣬��Ӧ���ٶȷֱ�Ϊv1��v2��v3����֪С�����ˮƽ�森б�漰Բ����֮��Ķ�Ħ����������ͬ����С�����б��AB��ʱ���ٶ�Ϊv0����б��AC��ʱ���ٶ�ΪvC��Բ����˵��ٶ�ΪvC�䣬��������ڹ���Ӵ����Ļ�е����ʧ��������
��ͼ��ʾ��б��AB��AC�ĵ�ͨ��һС��Բ����ˮƽ��������Բ����ADC�ֱ���б��AB��ˮƽ�����У�С����A�˷ֱ��ɾ�ֹ��б��AB��б��AC����ADC�»����Ҷ��ܾ���ˮƽ���ϵ�Q�㣬��Ӧ���ٶȷֱ�Ϊv1��v2��v3����֪С�����ˮƽ�森б�漰Բ����֮��Ķ�Ħ����������ͬ����С�����б��AB��ʱ���ٶ�Ϊv0����б��AC��ʱ���ٶ�ΪvC��Բ����˵��ٶ�ΪvC�䣬��������ڹ���Ӵ����Ļ�е����ʧ��������
 ��ͼ��ʾ��б��AB��AC�ĵ�ͨ��һС��Բ����ˮƽ��������Բ����ADC�ֱ���б��AB��ˮƽ�����У�С����A�˷ֱ��ɾ�ֹ��б��AB��б��AC����ADC�»����Ҷ��ܾ���ˮƽ���ϵ�Q�㣬��Ӧ���ٶȷֱ�Ϊv1��v2��v3����֪С�����ˮƽ�森б�漰Բ����֮��Ķ�Ħ����������ͬ����С�����б��AB��ʱ���ٶ�Ϊv0����б��AC��ʱ���ٶ�ΪvC��Բ����˵��ٶ�ΪvC�䣬��������ڹ���Ӵ����Ļ�е����ʧ��������
��ͼ��ʾ��б��AB��AC�ĵ�ͨ��һС��Բ����ˮƽ��������Բ����ADC�ֱ���б��AB��ˮƽ�����У�С����A�˷ֱ��ɾ�ֹ��б��AB��б��AC����ADC�»����Ҷ��ܾ���ˮƽ���ϵ�Q�㣬��Ӧ���ٶȷֱ�Ϊv1��v2��v3����֪С�����ˮƽ�森б�漰Բ����֮��Ķ�Ħ����������ͬ����С�����б��AB��ʱ���ٶ�Ϊv0����б��AC��ʱ���ٶ�ΪvC��Բ����˵��ٶ�ΪvC�䣬��������ڹ���Ӵ����Ļ�е����ʧ��������| A�� | v1��v2 | B�� | v2��v3 | C�� | vC=vC�� | D�� | vB=vC |
6��ԭ�ӵ�����������Ҫԭ�����˺��У�����һ��ԭ�Ӻ˷��������µ��ѱ䷴Ӧ��${\;}_{92}^{235}$U+${\;}_{0}^{1}$n��A+B+2${\;}_{0}^{1}$n��A+B�����ǣ�������
| A�� | ${\;}_{54}^{140}Xe+{\;}_{38}^{94}Sr$ | B�� | ${\;}_{54}^{140}Xe+{\;}_{36}^{93}Kr$ | ||
| C�� | ${\;}_{56}^{141}Ba+{\;}_{36}^{92}Kr$ | D�� | ${\;}_{56}^{141}Ba+{\;}_{38}^{93}Sr$ |
3�� ${\;}_{92}^{238}$U��һ�ַ�����Ԫ�أ��ܹ��Է��ؽ���һϵ�з�����˥�䣬��ͼ��ʾ������˵����ȷ���ǣ�������
${\;}_{92}^{238}$U��һ�ַ�����Ԫ�أ��ܹ��Է��ؽ���һϵ�з�����˥�䣬��ͼ��ʾ������˵����ȷ���ǣ�������
 ${\;}_{92}^{238}$U��һ�ַ�����Ԫ�أ��ܹ��Է��ؽ���һϵ�з�����˥�䣬��ͼ��ʾ������˵����ȷ���ǣ�������
${\;}_{92}^{238}$U��һ�ַ�����Ԫ�أ��ܹ��Է��ؽ���һϵ�з�����˥�䣬��ͼ��ʾ������˵����ȷ���ǣ�������| A�� | ͼ��a=84��b=206 | |
| B�� | ${\;}_{82}^{206}$Pb��${\;}_{92}^{238}$U�ıȽ���ܴ� | |
| C�� | Y�Ǧ�˥�䣬�ų����� | |
| D�� | ${\;}_{82}^{206}$Pb����������${\;}_{81}^{b}$Ti�Ķ� |
7�� 1772�꣬�����������ѧ���������������ġ��������⡷ָ�����������������������壨��̫���͵�������ͬһƽ������5������㣬��ͼ�е�L1��L2��L3��L4��L5��ʾ�����dz�Ϊ�������յ㣮��������λ����Щ���ϣ�����̫�������ͬ���������£����Լ���������ȼ�϶����������ͬ����̫����Բ���˶��������������������ԣ��Ѿ���Ϊ�������������̽��������ĵط���2012��8��25��23ʱ27�֣�����77��ķ��У����϶���š����������״�ʵ�ִ��������������ܿ�ȷ����������Լ150�������������L2�㣬����˵����ȷ���ǣ�������
1772�꣬�����������ѧ���������������ġ��������⡷ָ�����������������������壨��̫���͵�������ͬһƽ������5������㣬��ͼ�е�L1��L2��L3��L4��L5��ʾ�����dz�Ϊ�������յ㣮��������λ����Щ���ϣ�����̫�������ͬ���������£����Լ���������ȼ�϶����������ͬ����̫����Բ���˶��������������������ԣ��Ѿ���Ϊ�������������̽��������ĵط���2012��8��25��23ʱ27�֣�����77��ķ��У����϶���š����������״�ʵ�ִ��������������ܿ�ȷ����������Լ150�������������L2�㣬����˵����ȷ���ǣ�������
 1772�꣬�����������ѧ���������������ġ��������⡷ָ�����������������������壨��̫���͵�������ͬһƽ������5������㣬��ͼ�е�L1��L2��L3��L4��L5��ʾ�����dz�Ϊ�������յ㣮��������λ����Щ���ϣ�����̫�������ͬ���������£����Լ���������ȼ�϶����������ͬ����̫����Բ���˶��������������������ԣ��Ѿ���Ϊ�������������̽��������ĵط���2012��8��25��23ʱ27�֣�����77��ķ��У����϶���š����������״�ʵ�ִ��������������ܿ�ȷ����������Լ150�������������L2�㣬����˵����ȷ���ǣ�������
1772�꣬�����������ѧ���������������ġ��������⡷ָ�����������������������壨��̫���͵�������ͬһƽ������5������㣬��ͼ�е�L1��L2��L3��L4��L5��ʾ�����dz�Ϊ�������յ㣮��������λ����Щ���ϣ�����̫�������ͬ���������£����Լ���������ȼ�϶����������ͬ����̫����Բ���˶��������������������ԣ��Ѿ���Ϊ�������������̽��������ĵط���2012��8��25��23ʱ27�֣�����77��ķ��У����϶���š����������״�ʵ�ִ��������������ܿ�ȷ����������Լ150�������������L2�㣬����˵����ȷ���ǣ�������| A�� | ���϶���š���̫���˶����ں͵�����ת������� | |
| B�� | ���϶���š���L2�㴦��ƽ��״̬ | |
| C�� | ���϶���š���̫���˶������ļ��ٶȴ��ڵ�����̫���˶������ļ��ٶ� | |
| D�� | ���϶���š���L2������̫���͵��������ĺ�������L1��С |
4��������������ȷ���ǣ�������
| A�� | ��֪ˮ��Ħ��������ˮ���ӵ����������Լ���������ӵ����� | |
| B�� | �����˶����Ƿ��ӵ������˶� | |
| C�� | �������������������ܲ�һ������ | |
| D�� | ���Ӽ������������ŷ��Ӽ���������һ���ȼ�С������ | |
| E�� | �û���ѹ�������ڵ��������壬����������3.0��105J�Ĺ���ͬʱ���������ų�1.5��105J������������������������1.5��105J |
4�� ��ͼ��ʾ����ˮƽ���ҡ���СΪE����ǿ�糡�У���O��̶�һ�����ΪQ������ɣ�A��B��C��DΪ��OΪԲ�ġ��뾶Ϊr��ͬһԲ���ϵ��ĵ㣬B��D������糡��ƽ�У�A��C������糡�ߴ�ֱ��������
��ͼ��ʾ����ˮƽ���ҡ���СΪE����ǿ�糡�У���O��̶�һ�����ΪQ������ɣ�A��B��C��DΪ��OΪԲ�ġ��뾶Ϊr��ͬһԲ���ϵ��ĵ㣬B��D������糡��ƽ�У�A��C������糡�ߴ�ֱ��������
 ��ͼ��ʾ����ˮƽ���ҡ���СΪE����ǿ�糡�У���O��̶�һ�����ΪQ������ɣ�A��B��C��DΪ��OΪԲ�ġ��뾶Ϊr��ͬһԲ���ϵ��ĵ㣬B��D������糡��ƽ�У�A��C������糡�ߴ�ֱ��������
��ͼ��ʾ����ˮƽ���ҡ���СΪE����ǿ�糡�У���O��̶�һ�����ΪQ������ɣ�A��B��C��DΪ��OΪԲ�ġ��뾶Ϊr��ͬһԲ���ϵ��ĵ㣬B��D������糡��ƽ�У�A��C������糡�ߴ�ֱ��������| A�� | B��ij�ǿ��СΪE-k$\frac{Q}{{r}^{2}}$ | B�� | A��ij�ǿ��СΪ$\sqrt{{E}^{2}+{K}^{2}\frac{{Q}^{2}}{{r}^{4}}}$ | ||
| C�� | D��ij�ǿ��С������Ϊ0 | D�� | A��C����ij�ǿ��ͬ |