题目内容
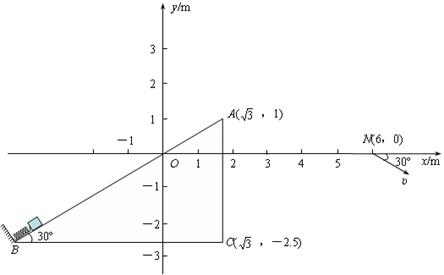
(19分)在竖直平面内存在如图所示的绝缘轨道,一质量为m=0.4kg、带电量为q=+0.4C的小滑块(可视为质点)在外力作用下压缩至离B点0.05m,此时弹性势能 =17.25J,弹簧一端固定在底端,与小滑块不相连,弹簧原长为2.05m,轨道与滑块间的动摩擦因数
=17.25J,弹簧一端固定在底端,与小滑块不相连,弹簧原长为2.05m,轨道与滑块间的动摩擦因数 .某时刻撤去外力,经过一段时间弹簧恢复至原长,再经过1.8s,同时施加电场和磁场,电场平行于纸面,且垂直x轴向上,场强E=10N/C;磁场方向垂直于纸面,且仅存在于第二、三象限内,最终滑块到达N(6m,0)点,方向与水平方向成30º斜向下.(答案可用π表示,
.某时刻撤去外力,经过一段时间弹簧恢复至原长,再经过1.8s,同时施加电场和磁场,电场平行于纸面,且垂直x轴向上,场强E=10N/C;磁场方向垂直于纸面,且仅存在于第二、三象限内,最终滑块到达N(6m,0)点,方向与水平方向成30º斜向下.(答案可用π表示, )
)
(1)求弹簧完全恢复瞬间,小滑块的速度;
(2)求弹簧原长恢复后1.8s时小滑块所在的位置;
(3)求小滑块在磁场中的运动的时间.
 =17.25J,弹簧一端固定在底端,与小滑块不相连,弹簧原长为2.05m,轨道与滑块间的动摩擦因数
=17.25J,弹簧一端固定在底端,与小滑块不相连,弹簧原长为2.05m,轨道与滑块间的动摩擦因数 .某时刻撤去外力,经过一段时间弹簧恢复至原长,再经过1.8s,同时施加电场和磁场,电场平行于纸面,且垂直x轴向上,场强E=10N/C;磁场方向垂直于纸面,且仅存在于第二、三象限内,最终滑块到达N(6m,0)点,方向与水平方向成30º斜向下.(答案可用π表示,
.某时刻撤去外力,经过一段时间弹簧恢复至原长,再经过1.8s,同时施加电场和磁场,电场平行于纸面,且垂直x轴向上,场强E=10N/C;磁场方向垂直于纸面,且仅存在于第二、三象限内,最终滑块到达N(6m,0)点,方向与水平方向成30º斜向下.(答案可用π表示, )
)(1)求弹簧完全恢复瞬间,小滑块的速度;
(2)求弹簧原长恢复后1.8s时小滑块所在的位置;
(3)求小滑块在磁场中的运动的时间.

(1)7.5m/s (2)小滑块此时刚好到达坐标原点(3)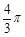 s
s
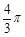 s
s 试题分析:(1)如图所示,弹簧释放到恢复原长经过位移s到达D点,根据能量关系,有:
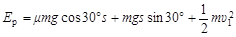 (2分)
(2分)其中
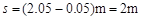
解得:
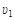 =7.5m/s (1分)
=7.5m/s (1分)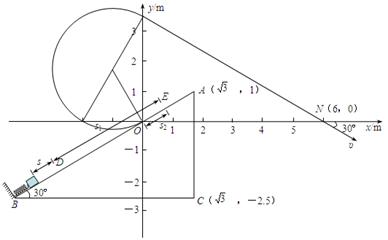
(2)此后小滑块沿斜面向上做减速运动,由牛顿第二定律得:
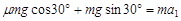 (2分)
(2分)解得小滑块的加速度大小为:
 =7.5
=7.5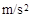 (1分)
(1分)设小滑块运动到E点的速度为0,上升的位移为
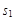 ,则运动时间为:
,则运动时间为: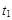 =
=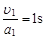 (1分)
(1分)上升的位移为:
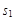 =
=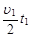 =3.75m (1分)
=3.75m (1分)接着小滑块沿斜面下滑,运动时间为:
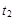 =(1.8-1)s=0.8s
=(1.8-1)s=0.8s由牛顿第二定律有:
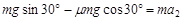 (1分)
(1分)解得:
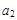 =2.5
=2.5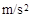 (1分)
(1分)则下滑的位移为:
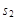 =
=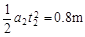 (1分)
(1分)由图中几何关系知:BD+
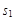 =BO+
=BO+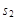 (1分)
(1分)即小滑块此时刚好到达坐标原点. (1分)
(3)施加电场和磁场后,由题中数据知:
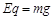
即小滑块只受洛伦兹力作用,做圆周运动到P(0,
 m)点,然后做匀速直线运动运动到N(6m,0).
m)点,然后做匀速直线运动运动到N(6m,0).小滑块进入磁场的速度为:
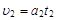 =2m/s
=2m/s洛伦兹力提供向心力:
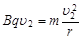 (2分)
(2分)由图中几何关系知小滑块做圆周运动的半径为:r=2m (2分)
解得:
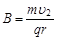 =1T (1分)
=1T (1分)运动周期为:
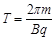
在磁场中运动的时间为:
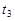 =
=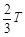 =
=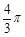 s (1分)
s (1分)
练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目



 试推导出电子比荷
试推导出电子比荷 的表达式;
的表达式; ,0),在y轴与直线MN之间的区域内,存在垂直于xOy平面向外、磁感应强度为B的匀强磁场。在直角坐标系xOy的第Ⅳ象限区域内存在沿y轴,正方向、大小为
,0),在y轴与直线MN之间的区域内,存在垂直于xOy平面向外、磁感应强度为B的匀强磁场。在直角坐标系xOy的第Ⅳ象限区域内存在沿y轴,正方向、大小为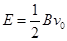 的匀强电场,在x=3a处垂直于x轴放置一平面荧光屏,与x轴交点为Q,电子束以相同的速度v0从y轴上0
的匀强电场,在x=3a处垂直于x轴放置一平面荧光屏,与x轴交点为Q,电子束以相同的速度v0从y轴上0 y
y ;
;
 .现将一质量为m、带电量为-q(q>0)的小环套在PQ杆上,小环所受的电场力大小为其重力的3倍.(重力加速度为g).求:
.现将一质量为m、带电量为-q(q>0)的小环套在PQ杆上,小环所受的电场力大小为其重力的3倍.(重力加速度为g).求:
 )d,板间距离为2d,在两板间有一圆形匀强磁场区域,磁场边界与两板及右侧边缘线相切,P点是磁场边界与下板N的切点,磁场方向垂直于纸面向里,现有一带电微粒从板的左侧进入磁场,若微粒从两板的正中间以大小为v0水平速度进入板间电场,恰做匀速直线运动,经圆形磁场偏转后打在P点。
)d,板间距离为2d,在两板间有一圆形匀强磁场区域,磁场边界与两板及右侧边缘线相切,P点是磁场边界与下板N的切点,磁场方向垂直于纸面向里,现有一带电微粒从板的左侧进入磁场,若微粒从两板的正中间以大小为v0水平速度进入板间电场,恰做匀速直线运动,经圆形磁场偏转后打在P点。


 后进入Ⅱ区.已知Ⅰ区的磁感应强度的大小为B,Ⅱ区的电场强度大小为2Bv0,不计粒子重力.求:
后进入Ⅱ区.已知Ⅰ区的磁感应强度的大小为B,Ⅱ区的电场强度大小为2Bv0,不计粒子重力.求:
 ;
;