Question

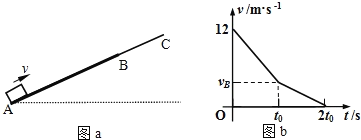
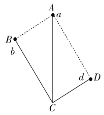
【题目】如图，光滑细杆BC、DC和AC构成矩形ABCD的两邻边和对角线，AC∶BC∶DC＝5∶4∶3，AC杆竖直，各杆上分别套有一质点小球a、b、d，a、b、d三小球的质量比为1∶2∶3，现让三小球同时从各杆的顶点由静止释放，不计空气阻力，则a、b、d三小球在各杆上滑行的时间之比为( 　　)

A. 1∶1∶1 B. 5∶4∶3 C. 5∶8∶9 D. 1∶2∶3

Answer 1

【答案】A

【解析】

由几何知识求出出三个小球的位移表达式，由牛顿第二定律求出两球的加速度a表达式，再由位移公式求解滑行时间之比；

设，，,a、b、d三小球在各杆上滑行的时间分别为，加速度分别为。
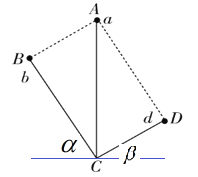
由几何知识得，BC的倾角为，DC的倾角为，如图所示：

a球为自由下过程，
由，得
根据牛顿第二定律得：
沿BC下滑的小球，加速度为
由位移时间公式得：，得
沿DC下滑的小球，加速度为
由位移时间公式得：，得 ，所以，故选项A正确，选项BCD错误。