题目内容
(16分)如图所示,AB为固定在竖直平面内粗糙倾斜轨道,BC为光滑水平轨道,CD为固定在竖直平面内的光滑圆弧轨道,且AB与BC通过一小段光滑弧形轨道相连,BC与弧CD相切。已知AB长为L=10m,倾角θ=37°,BC长s= m,CD弧的半径为R=
m,CD弧的半径为R= m,O为其圆心,∠COD=143°。整个装置处在水平向左的匀强电场中,电场强度大小为E=1×103N/C。一质量为m=0.4kg、电荷量为q= +3×10 -3C的物体从A点以初速度vA=15m/s沿AB轨道开始运动。若物体与轨道AB间的动摩擦因数为μ=0.2,sin37°=0.6,cos37°=0.8,g=10m/s2,物体运动过程中电荷量不变。求
m,O为其圆心,∠COD=143°。整个装置处在水平向左的匀强电场中,电场强度大小为E=1×103N/C。一质量为m=0.4kg、电荷量为q= +3×10 -3C的物体从A点以初速度vA=15m/s沿AB轨道开始运动。若物体与轨道AB间的动摩擦因数为μ=0.2,sin37°=0.6,cos37°=0.8,g=10m/s2,物体运动过程中电荷量不变。求
(1)物体在AB轨道上运动时,重力和电场力对物体所做的总功;
(2)物体能否到达D点;
(3)物体离开CD轨道后运动的最高点相对于O点的水平距离x和竖直距离y。
 m,CD弧的半径为R=
m,CD弧的半径为R= m,O为其圆心,∠COD=143°。整个装置处在水平向左的匀强电场中,电场强度大小为E=1×103N/C。一质量为m=0.4kg、电荷量为q= +3×10 -3C的物体从A点以初速度vA=15m/s沿AB轨道开始运动。若物体与轨道AB间的动摩擦因数为μ=0.2,sin37°=0.6,cos37°=0.8,g=10m/s2,物体运动过程中电荷量不变。求
m,O为其圆心,∠COD=143°。整个装置处在水平向左的匀强电场中,电场强度大小为E=1×103N/C。一质量为m=0.4kg、电荷量为q= +3×10 -3C的物体从A点以初速度vA=15m/s沿AB轨道开始运动。若物体与轨道AB间的动摩擦因数为μ=0.2,sin37°=0.6,cos37°=0.8,g=10m/s2,物体运动过程中电荷量不变。求(1)物体在AB轨道上运动时,重力和电场力对物体所做的总功;
(2)物体能否到达D点;
(3)物体离开CD轨道后运动的最高点相对于O点的水平距离x和竖直距离y。

(1)0(2)不能到达D点 (3)2.05m
试题分析:(1)物体所受重力和电场力的合力大小为
 (1分)
(1分)合力与竖直方向的夹角为α

 (1分)
(1分)所以物体在轨道AB上运动时重力和电场力对物体做的总功为W=0 (1分)
(2)D点为CD轨道上的等效最高点,设物体能到D点,其速度为vD
对物体由A到D的过程由动能定理得
 (2分)
(2分)设物体刚能到D点时速度为v0
由牛顿第二定律得
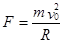 (2分)
(2分)解得v0>vD
因此物体不能到达D点 (1分)
(3)物体刚要离开轨道时轨道对物体的弹力为零,设此时物体位置与O点连线与竖直方向的夹角为β,物体速度为v
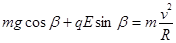 (2分)
(2分)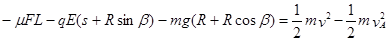 (2分)
(2分)解得v=5m/s,sinβ=0.8 (1分)
物体离开轨道后做斜抛运动,设其到最高点的时间为t
vsinβ= gt
t=0.4s (1分)
物体运动的最高点相对O点的水平距离、竖直距离分别为
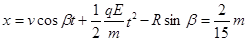 (1分)
(1分)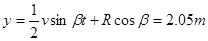 (1分)
(1分)点评:本题难度较大,属于多过程问题,其中涉及到了重力和电场力做功,和圆周运动的临界问题,利用动能定理解题时找到初末状态,刚好通过圆周最高点的临界速度不为零,而是由重力提供向心力

练习册系列答案
相关题目


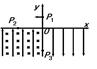



 m,导轨平面与水平面成
m,导轨平面与水平面成 角,上端连接阻值为
角,上端连接阻值为 的电阻.匀强磁场方向与导轨平面垂直,磁感应强度
的电阻.匀强磁场方向与导轨平面垂直,磁感应强度 T.质量为
T.质量为 kg、电阻为
kg、电阻为 的金属棒
的金属棒 ,以初速度
,以初速度 从导轨底端向上滑行,金属棒
从导轨底端向上滑行,金属棒 的共同作用下做匀变速直线运动,速度-时间图像如图所示.设金属棒与导轨垂直并保持良好接触,它们之间的动摩擦因数为
的共同作用下做匀变速直线运动,速度-时间图像如图所示.设金属棒与导轨垂直并保持良好接触,它们之间的动摩擦因数为 .(
.( m/s2,
m/s2, ,
, ),求:
),求:
 消耗的最大功率?
消耗的最大功率?