��Ŀ����
����Ŀ��Ϊ����֤��ײ�еĶ����غ�ͼ�������С�����ײ�Ƿ�Ϊ������ײ��ijͬѧѡȡ�������ͬ���������Ƚϴ��С������������������ʵ�飺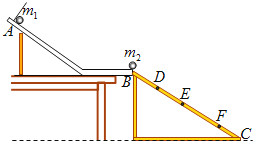
������ƽ�������С��������ֱ�Ϊm1��m2 �� ��m1��m2 ��
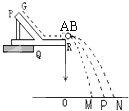
�ڰ���ͼ��ʾ��װ��ʵ��װ�ã���б��AA�̶������ߣ�ʹ�۵�ĩ�˵������ˮƽ����һб��AC������б��ĩ�ˣ�
���Ȳ���С��m2 �� ��С��m1��б�۶���A���ɾ�ֹ��ʼ���£�����С����б���ϵ����λ�ã�
�ܽ�С��m2����б��ǰ�˱�Ե������С��m1��б�۶���A�����£�ʹ���Ƿ�����ײ���ֱ����С��m1��С��m2��б���ϵ����λ�ã�
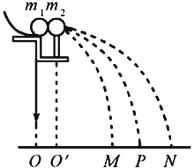
���ú��̶ȳ������������λ�õ�б��ĩ�˵�A�ľ��룮ͼ��D��E��F���Ǹ�ͬѧ���µ�С����б���ϵļ������λ�ã���A��ľ���ֱ�ΪLD��LE��LF ��
���ݸ�ͬѧ��ʵ�飬�ش��������⣺
a�ڲ���С��m2ʱ��С��m1��б�۶���A���ɾ�ֹ��ʼ���£�m1�������ͼ�еĵ�����С��m2����б��ĩ�˱�Ե����С��m1��б�۶���A���ɾ�ֹ��ʼ���£�ʹ���Ƿ�����ײ������С��m1�������ͼ�еĵ� ��
b����ײ�����У������ͻ�е�ܾ��غ㣬���ƿ��������������б���ʽ����ȷ���� ��
a��m1LF=m1LD+m2LE
b��m1LE2=m1LD2+m2LF2
c��m1LE=m1LD+m2LF
d��LE=LF��LD ��
���𰸡�E��D��c
����������1��С��m1��б�۶���A���ɾ�ֹ��ʼ���£�m1�������ͼ�е�E�㣬С��m1��С��m2��ײ��С��m2���ٶ�����С��m1���ٶȼ�С������ƽ���˶���������ײ��m1�����ص���D�㣬m2�����ص���F�㣻��2����ײǰ��С��m1����ͼ�е�E�㣬����ˮƽ���ٶ�Ϊv1 �� С��m1��m2������ײ��m1�������ͼ�е�D�㣬����ˮƽ���ٶ�Ϊv1�䣬m2�������ͼ�е�F�㣬����ˮƽ���ٶ�Ϊv2 �� ��б��AC��ˮƽ������Ϊ�� �� ��ƽ���˶����ɵã�LDsin��= ![]() gt2 �� LDcos��=v1��t ��
gt2 �� LDcos��=v1��t ��
��ã�![]() ��ͬ���ɽ�ã�
��ͬ���ɽ�ã�![]() ��
��![]() ��
��
����ֻҪ����m1v1=m2v2+m1v1�䣬���ٶ�v���������ã�m1![]() =m1
=m1![]() +m2
+m2![]() ��˵��������ײ�����ж����غ㣻
��˵��������ײ�����ж����غ㣻
����С�����ײ�ǵ�����ײ������ײǰ���е��û����ʧ����Ҫ�����ϵʽ�� ![]() m1v12=
m1v12= ![]() m1v1��2+
m1v1��2+![]() m2v22 ��
m2v22 ��
�����ã���m1LE=m1LD+m2LF �� ��C��ȷ����ѡC ��
���Դ���Ϊ����1��E��D����2��C ��
�����㾫�����������⣬������Ҫ�˽���غ㶨��(�����غ㶨�ɳ�����������ϵͳ����������ϵͳ���������ĺ���Ϊ�㣻ϵͳ���ܵ������ĺ����䲻Ϊ�㣬��ϵͳ����������С�öࣻϵͳ���������ĺ����䲻Ϊ�㣬����ij�������ϵķ���Ϊ�㣬���ڸ÷�����ϵͳ���ܶ����ķ������ֲ���)��