题目内容
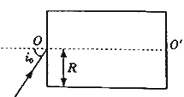
【题目】半径为R、介质折射率为n的透明圆柱体，过其轴线OO’的截面如图所示．位于截面所在平面内的一细束光线，以角i0由O点入射，折射光线由上边界的A点射出．当光线在O点的入射角减小至某一值时，折射光线在上边界的B点恰好发生全反射．求A、B两点间的距离．
【答案】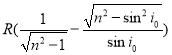
【解析】
试题由折射定律求出光线在左侧面上的折射角，可几何关系求出A、D间的距离．由sinC=
求出全反射临界角C，再由几何知识求解B、D间的距离，即可得到AB间的距离．
解：当光线在O点的入射角为i0时，设折射角为r0，由折射定律得：
=n
设AD间的距离为d1，由几何关系得：
sinr0=
若光线在B点恰好发生全反射，则在B点的入射角恰好等于临界角C，设BD间的距离为d2．则有：
sinC=
由几何关系得：sinC=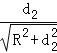
则A、B两点间的距离为：d=d2﹣d1；
联立解得：d=（
﹣
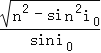）R
答：A、B两点间的距离为（
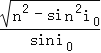﹣）R．
练习册系列答案
相关题目
