Question

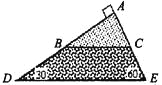
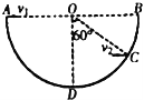
【题目】如图所示，水平地面上有一个坑，其竖直截面为半圆，O为圆心，AB为沿水平方向的直径，若在A点以某一初速度沿水平方向平抛一小球1，小球1将击中坑壁上的最低点D点，同时，在C点水平抛出另一相同质量的小球2，小球2也能击中D点，已知CD弧对应的圆心角为60°，不计空气阻力，则（　　）

A. 小球1与2的初速度之比

B. 小球1与2的初速度之比

C. 小球1与2在此过程中动能的增加量之比为2：1

D. 在击中D点前瞬间，重力对小球1与2做功的瞬时功率之比为

Answer 1

【答案】BCD

【解析】

根据平抛运动的竖直位移研究运动的时间，根据水平位移求出平抛运动的初速度．从而得出两球的初速度之比．平抛运动过程中，重力做功等于动能的增加量，由W=mgh分析动能增加量的关系．重力的瞬时功率根据公式P=mgvy研究．

设半圆的半径为R．小球从A点平抛，可得：R=v1t1；R=gt12；小球从C点平抛，可得：Rsin60°=v2t2；R（1-cos60°）=gt22；联立解得：v1：v2=．故A错误，B正确。根据动能定理得知：重力做的功等于动能的增加量，则得：小球1与2在此过程中动能的增加量之比为 mgR：mgR（1-cos60°）=2：1．故C正确。两球均做平抛运动，竖直方向做自由落体运动，由h=gt2，得，在击中D点前瞬间，重力做功的功率为P=mgvy=mggt=mg2=mg，则在击中D点前瞬间，重力对小球1与2做功的瞬时功率之比为P1：P2==：1．故D正确；故选BCD。