题目内容
两根水平平行固定的光滑金属导轨宽为L,足够长,在其上放置两根长也为L且与导轨垂直的金属棒ab和cd,它们的质量分别为2m、m,电阻阻值均为R(金属导轨及导线的电阻均可忽略不计),整个装置处在磁感应强度大小为B、方向竖直向下的匀强磁场中.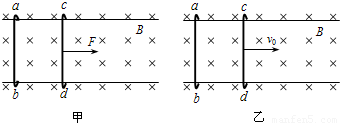
(1)现把金属棒ab锁定在导轨的左端,如图甲,对cd施加与导轨平行的水平向右的恒力F,使金属棒cd向右沿导轨运动,当金属棒cd的运动状态稳定时,金属棒cd的运动速度是多大?
(2)若对金属棒ab解除锁定,如图甲,对cd施加与导轨平行的水平向右的恒力F,使金属棒cd向右沿导轨运动,简述金属棒ab和金属棒cd的运动情况,求出整个电路最终的发热功率?
(3)若对金属棒ab解除锁定,如图乙,使金属棒cd获得瞬时水平向右的初速度v,当它们的运动状态达到稳定的过程中,金属棒ab中产生的热量是多少?
【答案】分析:(1)当cd棒稳定时,所受的安培力和恒力平衡,根据平衡,结合切割产生的感应电动势公式、闭合电路欧姆定律和安培力公式求出金属棒cd的运动速度.
(2)cd棒做初速为零加速度逐渐减小的加速运动,ab棒做初速为零加速度逐渐增大的加速运动,当两者加速度相等时,二者一起做加速度相等的匀加速直线运动.根据牛顿第二定律,结合安培力公式求出最终电路中的电流,通过发热功率公式求出整个电路的发热功率.
(3)ab棒在安培力作用下加速运动,而cd在安培力作用下减速运动,当它们的速度相同,达到稳定状态时,回路中的电流消失,ab,cd棒开始匀速运动.根据动量守恒定律和能量守恒定律求出金属棒ab中产生的热量.
解答:解:(1)当cd棒稳定时,恒力F和安培力大小相等,方向相反,以速度v匀速度运动,有:
F=BIL
又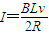 …
…
联立得: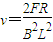
(2)cd棒做初速为零加速度逐渐减小的加速运动,ab棒做初速为零加速度逐渐增大的加速运动,当两者加速度相等时,二者一起做加速度相等的匀加速直线运动.设最终二者的加速度为a,则由牛顿第二定律:F=3ma,FA=2ma,
又由于 FA=BIL
发热功率 P=I22R
所以发热功率
(3)ab棒在安培力作用下加速运动,而cd在安培力作用下减速运动,当它们的速度相同,达到稳定状态时,回路中的电流消失,ab,cd棒开始匀速运动.
由动量守恒得:mv=3mv
由能量守恒得:电路中的发热量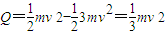
金属棒ab中产生的热量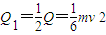
答:(1)当金属棒cd的运动状态稳定时,金属棒cd的运动速度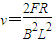 .
.
(2)整个电路最终的发热功率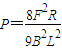 .
.
(3)金属棒ab中产生的热量是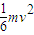 .
.
点评:本题综合考查了牛顿第二定律、闭合电路欧姆定律、动量守恒定理和能量守恒定律等,综合性较强,关键理清过程,选择合适的规律进行求解.
(2)cd棒做初速为零加速度逐渐减小的加速运动,ab棒做初速为零加速度逐渐增大的加速运动,当两者加速度相等时,二者一起做加速度相等的匀加速直线运动.根据牛顿第二定律,结合安培力公式求出最终电路中的电流,通过发热功率公式求出整个电路的发热功率.
(3)ab棒在安培力作用下加速运动,而cd在安培力作用下减速运动,当它们的速度相同,达到稳定状态时,回路中的电流消失,ab,cd棒开始匀速运动.根据动量守恒定律和能量守恒定律求出金属棒ab中产生的热量.
解答:解:(1)当cd棒稳定时,恒力F和安培力大小相等,方向相反,以速度v匀速度运动,有:
F=BIL
又
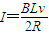 …
…联立得:
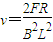
(2)cd棒做初速为零加速度逐渐减小的加速运动,ab棒做初速为零加速度逐渐增大的加速运动,当两者加速度相等时,二者一起做加速度相等的匀加速直线运动.设最终二者的加速度为a,则由牛顿第二定律:F=3ma,FA=2ma,
又由于 FA=BIL
发热功率 P=I22R
所以发热功率

(3)ab棒在安培力作用下加速运动,而cd在安培力作用下减速运动,当它们的速度相同,达到稳定状态时,回路中的电流消失,ab,cd棒开始匀速运动.
由动量守恒得:mv=3mv
由能量守恒得:电路中的发热量
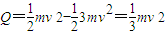
金属棒ab中产生的热量
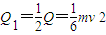
答:(1)当金属棒cd的运动状态稳定时,金属棒cd的运动速度
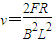 .
.(2)整个电路最终的发热功率
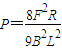 .
.(3)金属棒ab中产生的热量是
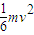 .
.点评:本题综合考查了牛顿第二定律、闭合电路欧姆定律、动量守恒定理和能量守恒定律等,综合性较强,关键理清过程,选择合适的规律进行求解.

练习册系列答案
相关题目




 (2011?泗阳县一模) (选做题)本题包括A、B、C三小题,请选定其中两题,并在相应答题区域内作答.若三题都做,则按A、B两题评分.
(2011?泗阳县一模) (选做题)本题包括A、B、C三小题,请选定其中两题,并在相应答题区域内作答.若三题都做,则按A、B两题评分. (3)图2示是一透明的圆柱体的横截面,其半径R=20cm,折射率为
(3)图2示是一透明的圆柱体的横截面,其半径R=20cm,折射率为