题目内容
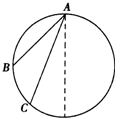
如图,从竖直面上大圆(直径d)的最高点A,引出两条不同的光滑轨道,端点都在大圆上,同一物体由静止开始,从A点分别沿两条轨道滑到底端,则( )
| A.到达底端的动能相等 | B.重力做功都相同 |
| C.机械能都相同 | D.所用的时间相同 |

A、同一物体从静止到达底端的动能,由动能定理可知,重力做功的不一样,所以它们到达底端的动能不同.故A错误;
B、同一物体从不同的光滑斜面下滑,重力做功的多少由高度决定,由于高度的不一,所以重力做功也不相同,故B错误;
C、同一物体由静止开始,从A点分别沿两条轨道滑到底端,由于均是光滑斜面,所以只有重力做功,因此机械能守恒.取静止释放处为零重力势能,则两者机械能相等.故C正确;
D、对物体在斜面上受力分析,由牛顿第二定律可求得,a=gcosα;根据运动学公式x=
| 1 |
| 2 |
| 1 |
| 2 |
故选CD.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目