题目内容
4. 如图所示,质量为M的长木块A静止于光滑水平面上,在其水平的上表面左端放一质量为m的滑块B,已知木块长为L,它与滑块之间的动摩擦因数为μ.现用水平向右的恒力F拉滑块B.若B从A的右端滑出,求:
如图所示,质量为M的长木块A静止于光滑水平面上,在其水平的上表面左端放一质量为m的滑块B,已知木块长为L,它与滑块之间的动摩擦因数为μ.现用水平向右的恒力F拉滑块B.若B从A的右端滑出,求:(1)长木块A的位移以及运动时间;
(2)求上述过程中恒力F做的功.
分析 (1)根据牛顿第二定律求的AB的加速度,根据运动学公式求的位移和时间;
(2)根据W=Fx求的拉力F做功
解答 解:(1)物块B的加速度为${a}_{B}=\frac{F-μmg}{m}$,A的加速度为${a}_{A}=\frac{μmg}{M}$
设经过时间t脱离,则B的位移为${x}_{B}=\frac{1}{2}{a}_{B}{t}^{2}$,A的位移${x}_{A}={\frac{1}{2}a}_{A}{t}^{2}$
L=xB-xA
联立解得$t=\sqrt{\frac{2Mmg}{MF-μm(M+m)g}}$,${x}_{A}=\frac{μ{m}^{2}{g}^{2}}{MF-μgm(M+m)}$,${x}_{B}=\frac{μ{m}^{2}{g}^{2}}{MF-μgm(M+m)}+L$
(2)拉力做功为W=FxB=$\frac{μ{m}^{2}{g}^{2}F}{MF-μgm(M+m)}+FL$
答:(1)长木块A的位移为$\frac{μ{m}^{2}{g}^{2}}{MF-μgm(M+m)}$,运动时间为$\sqrt{\frac{2Mmg}{MF-μm(M+m)g}}$;
(2)上述过程中恒力F做的功为$\frac{μ{m}^{2}{g}^{2}F}{MF-μgm(M+m)}+FL$
点评 本题主要考查了运动学公式,利用好运动学公式,抓住相对位移即可求得

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7. 距地面高5m的水平直轨道A、B两点相距2m,在B点用细线悬挂一小球,离地高度为h,如图.小车始终以4m/s的速度沿轨道匀速运动,经过A点时将随车携带的小球由轨道高度自由卸下,小车运动至B点时细线被轧断,最后两球同时落地.不计空气阻力,取重力加速度的大小1O.可求得h等于( )
距地面高5m的水平直轨道A、B两点相距2m,在B点用细线悬挂一小球,离地高度为h,如图.小车始终以4m/s的速度沿轨道匀速运动,经过A点时将随车携带的小球由轨道高度自由卸下,小车运动至B点时细线被轧断,最后两球同时落地.不计空气阻力,取重力加速度的大小1O.可求得h等于( )
 距地面高5m的水平直轨道A、B两点相距2m,在B点用细线悬挂一小球,离地高度为h,如图.小车始终以4m/s的速度沿轨道匀速运动,经过A点时将随车携带的小球由轨道高度自由卸下,小车运动至B点时细线被轧断,最后两球同时落地.不计空气阻力,取重力加速度的大小1O.可求得h等于( )
距地面高5m的水平直轨道A、B两点相距2m,在B点用细线悬挂一小球,离地高度为h,如图.小车始终以4m/s的速度沿轨道匀速运动,经过A点时将随车携带的小球由轨道高度自由卸下,小车运动至B点时细线被轧断,最后两球同时落地.不计空气阻力,取重力加速度的大小1O.可求得h等于( )| A. | 4.75m | B. | 3.75m | C. | 2.25m | D. | 1.25m |
12.某拱桥可以看成是一段圆弧,当汽车以10m/s的速度通过桥顶时,对桥顶的压力为车重的$\frac{3}{4}$倍,要使汽车对桥顶恰好没有压力,汽车的速度应为( )(g=10m/s2)
| A. | 15m/s | B. | 20m/s | C. | 25m/s | D. | 30m/s |
16.如图所示,某质点从静止开始做直线运动的加速度a-时间t图象为正弦曲线,由图可判断( )

| A. | 在0~t1时间内,质点的速率增大,在t1~t2时间内,质点的速率减小 | |
| B. | 若0~t2时间内质点沿正向运动,则t2~t4时间内沿负向运动 | |
| C. | 在0~t4时间内,物体的位移为零 | |
| D. | 在t4时刻,物体的速度为零 |
13.下列有关质点的说法中,正确的是( )
| A. | 当研究地球的自转时,可以将其看做质点 | |
| B. | 用GPS定位系统确定正在南极冰盖考察的某科考队员的位置时,该队员可看做质点 | |
| C. | 研究乒乓球在空中飞旋的轨迹时,不能将其看做质点 | |
| D. | 凡是小的物体,皆可看成质点;凡是大的物体,皆不能看成质点 |
 一根轻弹簧,其弹力F的大小与长度x的关系如图中的线段a和b所示,求:
一根轻弹簧,其弹力F的大小与长度x的关系如图中的线段a和b所示,求: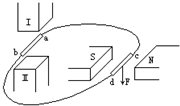 如图所示,Ⅰ和Ⅱ是一对异名磁极,ab为放在其间的金属棒,ab和cd用导线连成一个闭合回路.当ab棒向左运动时,cd导线受到向下的磁场力.由此可知cd导线中的电流方向是由c到d.(填“由d到c”或“由c到d”),Ⅰ是S极.
如图所示,Ⅰ和Ⅱ是一对异名磁极,ab为放在其间的金属棒,ab和cd用导线连成一个闭合回路.当ab棒向左运动时,cd导线受到向下的磁场力.由此可知cd导线中的电流方向是由c到d.(填“由d到c”或“由c到d”),Ⅰ是S极.


