题目内容
17.人类发射的空间探测器进入某行星的引力范围后,绕该行星做匀速圆周运动,已知该行星的半径为R,探测器运行轨道在其表面上空高为h处,运行周期为T,引力常量为G.求:(1)该行星的质量;
(2)探测器绕该行星运行时线速度的大小.
分析 (1)根据万有引力提供向心力即可求解行星质量;
(2)由圆周运动的公式$v=\frac{2πr}{T}$求线速度;
解答 解:(1)探测器绕行星做匀速圆周运动,万有引力提供向心力,有:
$G\frac{Mm}{(R+h)_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}(R+h)$
解得行星的质量:$M=\frac{4{π}_{\;}^{2}(R+h)_{\;}^{3}}{G{T}_{\;}^{2}}$
(2)由$v=\frac{2πr}{T}$
得:$v=\frac{2π(R+h)}{T}$
答:(1)该行星的质量为$\frac{4{π}_{\;}^{2}(R+h)_{\;}^{3}}{G{T}_{\;}^{2}}$;
(2)探测器绕该行星运行时线速度的大小$\frac{2π(R+h)}{T}$
点评 解决此题的关键是一定明确万有引力提供向心力,会用周期表示向心力,同时注意公式间的化简.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.第一个准确测量出万有引力常量的科学家是( )
| A. | 开普勒 | B. | 第谷 | C. | 牛顿 | D. | 卡文迪许 |
12.在物理学理论建立的过程中,有许多伟大的科学家做出了贡献,关于科学家和他们的贡献,下列说法中正确的是( )
| A. | 在对自由落体运动的研究中,伽利略猜想运动速度与下落时间成正比,并直接用实验进行了验证 | |
| B. | 法拉第通过实验研究,发现了电磁感应现象 | |
| C. | 库仑在研究电荷间相互作用时,提出了“电场”的概念 | |
| D. | 卡文迪许发现了电荷之间的相互作用规律,并测出了静电力常量k的值 |
2.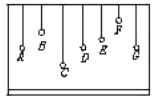 在张紧的水平柔绳上挂7个单摆,其中D摆的质量远大于其它摆的质量,先让D摆振动起来,其余各摆也会随之振动,已知A、D、G三摆的摆长相同,则下列判断正确的是( )
在张紧的水平柔绳上挂7个单摆,其中D摆的质量远大于其它摆的质量,先让D摆振动起来,其余各摆也会随之振动,已知A、D、G三摆的摆长相同,则下列判断正确的是( )
 在张紧的水平柔绳上挂7个单摆,其中D摆的质量远大于其它摆的质量,先让D摆振动起来,其余各摆也会随之振动,已知A、D、G三摆的摆长相同,则下列判断正确的是( )
在张紧的水平柔绳上挂7个单摆,其中D摆的质量远大于其它摆的质量,先让D摆振动起来,其余各摆也会随之振动,已知A、D、G三摆的摆长相同,则下列判断正确的是( )| A. | 7个单摆的固有频率都相同 | B. | 稳定后7个单摆的振动频率都相同 | ||
| C. | 除D摆外,A、G摆的振幅最大 | D. | 除D摆外,C、E摆的振幅最大 |
15.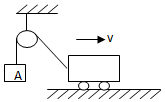 如图所示,在不计滑轮摩擦和绳子质量的条件下,当小车匀速向右运动时,物体A的受力情况是( )
如图所示,在不计滑轮摩擦和绳子质量的条件下,当小车匀速向右运动时,物体A的受力情况是( )
 如图所示,在不计滑轮摩擦和绳子质量的条件下,当小车匀速向右运动时,物体A的受力情况是( )
如图所示,在不计滑轮摩擦和绳子质量的条件下,当小车匀速向右运动时,物体A的受力情况是( )| A. | 绳的拉力小于A的重力 | B. | 绳的拉力等于A的重力 | ||
| C. | 绳的拉力大于A的重力 | D. | 绳的拉力大小不变 |
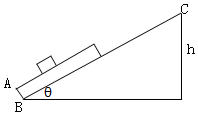 如图所示,倾角为θ=30o的光滑斜面上有固定挡板AB,斜面上B、C 两点间高度差为h.斜面上叠放着质量均为m的薄木板和小物块,木板长为L,下端位于挡板AB处,整体处于静止状态.木板和物块两者间的动摩擦因数μ=$\frac{\sqrt{3}}{2}$,最大静摩擦力等于滑动摩擦力.重力加速度为g.
如图所示,倾角为θ=30o的光滑斜面上有固定挡板AB,斜面上B、C 两点间高度差为h.斜面上叠放着质量均为m的薄木板和小物块,木板长为L,下端位于挡板AB处,整体处于静止状态.木板和物块两者间的动摩擦因数μ=$\frac{\sqrt{3}}{2}$,最大静摩擦力等于滑动摩擦力.重力加速度为g.  如图为某主题公园一种大型游戏机“跳楼机”.参加游戏的游客被安全带固定在座椅上,由电动机将座椅沿光滑的竖直轨道提升到离地面40m高处,然后由静止释放.为研究方便,可以认为座椅沿轨道做自由落体运动1.2s后,开始受到恒定阻力而立即做匀减速运动,且下落到离地面4m高处时速度刚好减小到零.然后再让座椅以相当缓慢的速度稳稳下落,将游客送回地面.取g=10m/s2.求:
如图为某主题公园一种大型游戏机“跳楼机”.参加游戏的游客被安全带固定在座椅上,由电动机将座椅沿光滑的竖直轨道提升到离地面40m高处,然后由静止释放.为研究方便,可以认为座椅沿轨道做自由落体运动1.2s后,开始受到恒定阻力而立即做匀减速运动,且下落到离地面4m高处时速度刚好减小到零.然后再让座椅以相当缓慢的速度稳稳下落,将游客送回地面.取g=10m/s2.求: ,(表的内阻已知)
,(表的内阻已知) ,(表的内阻未知)
,(表的内阻未知)
 、
、 表的示数分别记录为U1、U2;S闭合时,有示数的电压表其示数记为U,
表的示数分别记录为U1、U2;S闭合时,有示数的电压表其示数记为U, 表、
表、 表及滑动变阻器,并用伏安法测量了该电池的电动势和内阻,根据实验数据作出了相应的U-I图,如图所示,根据所作图线,可得出该电池E=1.48伏,r=0.86欧姆.
表及滑动变阻器,并用伏安法测量了该电池的电动势和内阻,根据实验数据作出了相应的U-I图,如图所示,根据所作图线,可得出该电池E=1.48伏,r=0.86欧姆.