题目内容
9. 如图为某主题公园一种大型游戏机“跳楼机”.参加游戏的游客被安全带固定在座椅上,由电动机将座椅沿光滑的竖直轨道提升到离地面40m高处,然后由静止释放.为研究方便,可以认为座椅沿轨道做自由落体运动1.2s后,开始受到恒定阻力而立即做匀减速运动,且下落到离地面4m高处时速度刚好减小到零.然后再让座椅以相当缓慢的速度稳稳下落,将游客送回地面.取g=10m/s2.求:
如图为某主题公园一种大型游戏机“跳楼机”.参加游戏的游客被安全带固定在座椅上,由电动机将座椅沿光滑的竖直轨道提升到离地面40m高处,然后由静止释放.为研究方便,可以认为座椅沿轨道做自由落体运动1.2s后,开始受到恒定阻力而立即做匀减速运动,且下落到离地面4m高处时速度刚好减小到零.然后再让座椅以相当缓慢的速度稳稳下落,将游客送回地面.取g=10m/s2.求:(1)座椅在自由下落结束时刻的速度大小?
(2)在匀减速阶段,座椅和游客的加速度大小.
分析 (1)由匀加速运动的速度公式直接求解;
(2)由匀变速的位移公式求得自由落体的位移,进而得到匀减速运动的位移,然后再根据匀变速运动的位移公式求得加速度.
解答 解:(1)座椅由静止自由下落1.2s,座椅在自由下落结束时刻的速度大小为:v=gt=12m/s;
(2)自由落体的位移为:${x}_{1}=\frac{1}{2}g{t}^{2}=\frac{1}{2}×10×1.{2}^{2}m=7.2m$
所以,匀减速阶段初速度v=12m/s,末速度为0,位移为:x=40-4-7.2(m)=28.8m,
那么在匀减速阶段,座椅和游客的加速度大小为:$a=\frac{{v}^{2}}{2x}=\frac{1{2}^{2}}{2×28.8}m/{s}^{2}=2.5m/{s}^{2}$;
答:(1)座椅在自由下落结束时刻的速度大小为12m/s;
(2)在匀减速阶段,座椅和游客的加速度大小为2.5m/s2.
点评 在初速度为零的匀变速直线运动中,位移$s=\frac{1}{2}a{t}^{2}=\frac{(at)^{2}}{2a}=\frac{{v}^{2}}{2a}$,我们常用v2=2as来求解运动速度而忽略中间求时间t的步骤.

练习册系列答案
相关题目
19.物体在几个力作用下保持静止,现只有一个力逐渐减小到零又逐渐增大到原值,则在力变化的整个过程中,物体加速度和速度大小变化的情况是( )
| A. | 加速度由零逐渐增大到某一数值后,又逐渐减小到零 | |
| B. | 速度由零逐渐增大到某一数值后,又逐渐减小到某一数值 | |
| C. | 速度由零逐渐增大到某一数值 | |
| D. | 加速度由零逐渐增大到某一数值 |
20.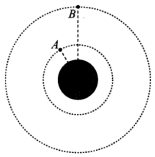 如图所示,A、B两颗卫星在同一平面内绕行星O沿逆时针方向做匀速圆周运动.若A、B的周期之比TA:TB=1:k (k为大于1的整数).从图示位置开始,在B运动一个周期的过程中( )
如图所示,A、B两颗卫星在同一平面内绕行星O沿逆时针方向做匀速圆周运动.若A、B的周期之比TA:TB=1:k (k为大于1的整数).从图示位置开始,在B运动一个周期的过程中( )
 如图所示,A、B两颗卫星在同一平面内绕行星O沿逆时针方向做匀速圆周运动.若A、B的周期之比TA:TB=1:k (k为大于1的整数).从图示位置开始,在B运动一个周期的过程中( )
如图所示,A、B两颗卫星在同一平面内绕行星O沿逆时针方向做匀速圆周运动.若A、B的周期之比TA:TB=1:k (k为大于1的整数).从图示位置开始,在B运动一个周期的过程中( )| A. | A、B距离最近的次数为k次 | B. | A、B距离最近的次数为k-1次 | ||
| C. | A、B与行星O共线的次数为2k | D. | A、B与行星O共线的次数为2k-1 |
8. 质量为m2,长度为L的小车静止在光滑水平面上,小车的左端站立着质量为m1的人.小车的右端站立着质量为m3的人,若m1>m3且两人从静止开始相向运动,互换位置,则此过程中小车的位移方向和大小为( )
质量为m2,长度为L的小车静止在光滑水平面上,小车的左端站立着质量为m1的人.小车的右端站立着质量为m3的人,若m1>m3且两人从静止开始相向运动,互换位置,则此过程中小车的位移方向和大小为( )
 质量为m2,长度为L的小车静止在光滑水平面上,小车的左端站立着质量为m1的人.小车的右端站立着质量为m3的人,若m1>m3且两人从静止开始相向运动,互换位置,则此过程中小车的位移方向和大小为( )
质量为m2,长度为L的小车静止在光滑水平面上,小车的左端站立着质量为m1的人.小车的右端站立着质量为m3的人,若m1>m3且两人从静止开始相向运动,互换位置,则此过程中小车的位移方向和大小为( )| A. | 小车左移,位移大小为$\frac{{m}_{1}+{m}_{3}}{{m}_{1}+{m}_{2}+{m}_{3}}$L | |
| B. | 小车左移,位移大小为$\frac{{m}_{1}-m3}{{m}_{1}+{m}_{2}+{m}_{3}}$L | |
| C. | 小车右移,位移大小为$\frac{({m}_{1}+{m}_{3})-{m}_{2}}{{m}_{1}+{m}_{2}+{m}_{3}}$L | |
| D. | 小车右移,位移大小为$\frac{{m}_{2}-({m}_{1}+{m}_{3})}{{m}_{1}+{m}_{2}+{m}_{3}}$L |
 在“验证碰撞中的质量守恒”实验中,某同学让质量为m1的小球从斜面上某处自由滚下与静止在斜槽末端质量为m2的小球发生对心碰撞,如图所示,回答下列问题:
在“验证碰撞中的质量守恒”实验中,某同学让质量为m1的小球从斜面上某处自由滚下与静止在斜槽末端质量为m2的小球发生对心碰撞,如图所示,回答下列问题: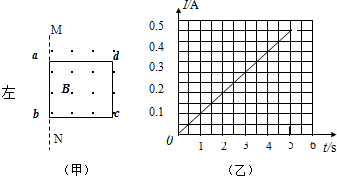
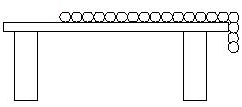 如图,长为L的铁链放在光滑的水平桌面上,有$\frac{1}{4}$的长度是悬在桌边外侧的,现这条链条由静止开始下滑,当链条刚好全部离开桌面时,链条的速率多少.
如图,长为L的铁链放在光滑的水平桌面上,有$\frac{1}{4}$的长度是悬在桌边外侧的,现这条链条由静止开始下滑,当链条刚好全部离开桌面时,链条的速率多少.