题目内容
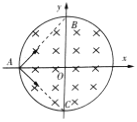
【题目】如图所示，在xOy平面内有一半径为r的圆形磁场区域，其内分布者磁感应强度为B方向垂直纸面向里的匀强磁场，圆形区域边界上放有圆形的感光胶片，粒子打在其上会感光。在磁区边界与x轴交点A处有一放射源A，以相同的速率发出质量为m、电量为+q的粒子沿垂直磁场方向进入磁场，其方向分布在由AB和AC所夹角度内，B和C为磁区边界与轴的两个交点。经过足够长的时间，结果光斑全部落在第II象限的感光胶片上，则下列这些速率中，满足题目情景的粒子的最大速率是
A. 
B. 
C. 
D. 
【答案】B
【解析】粒子在磁场中做圆周运动，洛伦兹力作向心力，所以有， 
，所以， 
；
因为粒子入射方向分布在由AB和AC所夹角度内，所以，粒子做圆周运动的圆心Q在AB的左侧，若粒子的出射点为P, 对于任一方向射出的粒子，∠OAQ不变，那么，AP越长，∠AOP越大，则∠AQP越小，半径R越大，所以，当P与B重合时，半径最大；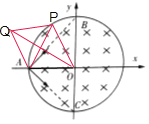
则有，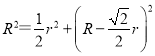 
，所以
；所以，这些粒子中速度最大值
，故B正确，ACD错误．故选B.
练习册系列答案
阅读快车系列答案
相关题目
