��Ŀ����
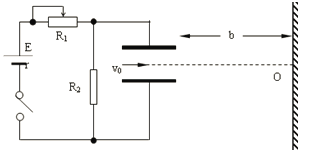
����Ŀ����ͼ��ʾ��ˮƽ���ʹ�A��B���˵����x=6m����v0=4m/s���ٶȣ�ʼ�ձ��ֲ��䣩˳ʱ���˶�����һСú�飨����Ϊ�ʵ㣩���ٶȵ������A�㴦����֪Сú���봫�ʹ���Ķ�Ħ������Ϊ0.2��gȡ10m/s2 �� ����Сú���봫�ʹ�֮������Ի��������ڴ��ʹ������»��ۣ���Сú���A�˶���B�Ĺ����У� ��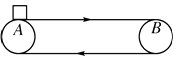
A.Сú���A�˶���B��ʱ����3s
B.���۳�����4m
C.Сú�鵽��B���ٶ��� ![]() m/s
m/s
D.Ƥ���˶��ľ�����10m
���𰸡�B,D
���������⣺A��Сú���ڴ��ʹ��ϻ���ʱ������ţ�ٵڶ������У���mg=ma��
��� a=2m/s2��
��ú���ٶȺʹ��ʹ��ٶ���ͬʱ������ʱ��Ϊ��t1= ![]() =
= ![]() =2s
=2s
ͨ����λ��Ϊ��x1= ![]() =
= ![]() m=4m��x=6m
m=4m��x=6m
��˹��ٺ�ú���洫�ʹ�һ�������˶���������ͬ���ٶ�Ϊ��v=4m/s��
�����˶���ʱ��Ϊ��t2= ![]() =
= ![]() s=0.5s��
s=0.5s��
���Сú���A�˶���B��ʱ��Ϊ��t=t1+t2=2.5s����A���������⣮
B�����۳���Ϊ��L=v0t1��x1=4��2��4=4m����B�������⣮
C��Сú�鵽��B���ٶ�Ϊ��v=v0=4m/s����C���������⣮
D��Ƥ���˶��ľ���Ϊ��x��=v0t=4��2.5m=10m����D��������
���Դ��ǣ�BD
�����㾫���������ȱ���ֱ���˶����ٶȡ�λ�ơ�ʱ��Ĺ�ϵ����Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪�ٶȹ�ʽ��V=V0+at��λ�ƹ�ʽ��s=v0t+1/2at2���ٶ�λ�ƹ�ʽ��vt2-v02=2as�����ϸ�ʽ��Ϊʸ��ʽ��Ӧ��ʱӦ�涨������Ȼ���ʸ����Ϊ��������⣬ͨ��ѡ���ٶȷ���Ϊ�������Ǹ�������һ�µ�ȡ��+��ֵ�����������෴��ȡ��-��ֵ��