Question

【题目】如图所示，CDF为间定在竖直平而内的圆弧轨道，圆心为O，半径OC与水平方向的 夹角=，C、E两点等高。一质量m=0.2kg的小物块（视为质点）在斜向上的拉力F作用下沿水平台面以大小v0=3m/s的速度做匀速直线运动，离开台面右端B后立即撤去力F，物块恰好从C点无碰撞地进人轨道CDE。已知物块通过E点的速度与通过C点时的速度大小相等，物块与台面间的动摩擦因数μ=0.75，取g=10 m/s2， sin= 0.6， cos=0.8，空气阻力不计。

（1）求力F的最小值Fmin；

（2）求B、C两点的水平距离x；

（3）若物块从E点飞出后恰好能回到C点，求物块通过E点前瞬间的角速度大小（结果可保留分式）。

Answer 1

【答案】（1）1.2N （2）1.2m （3）rad/s

【解析】

(1)小物块在水平面AB段受重力、支持力、摩擦力和拉力，做匀速直线运动，设拉力与水平方向夹角为α，根据平衡得

Fcosα=μ（mg-Fsinα）

解得

当sin（α+γ）=1时F最小，最小值为

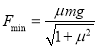
(2)C点速度分解如图所示：

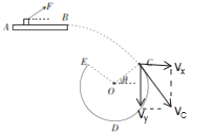
由几何关系得：

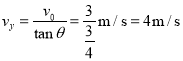
由B到C小物体做平抛运动，则：

联立解得：

xBC=1.2m

(3)由E到C做斜上抛运动，设运动时间为t′，圆轨道的半径为r，若物块从E点飞出后恰好能回到C点，则

联立解得