题目内容
11.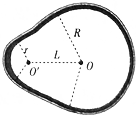 图示为赛车场的一个“梨形”水平赛道,两个弯道分别为半径R=60m的大圆弧和r=30m的小圆弧,直道与弯道相切.大、小圆弧圆心O、O′距离L=60m.赛车沿弯道路线行驶时,路面对轮胎的最大径向静摩擦力是赛车重力的2.25倍,假设赛车在直道上做匀变速直线运动,在弯道上做匀速圆周运动,重力加速度g=10m/s2,要使赛车绕赛道一周用时最短,下列说法正确的是( )
图示为赛车场的一个“梨形”水平赛道,两个弯道分别为半径R=60m的大圆弧和r=30m的小圆弧,直道与弯道相切.大、小圆弧圆心O、O′距离L=60m.赛车沿弯道路线行驶时,路面对轮胎的最大径向静摩擦力是赛车重力的2.25倍,假设赛车在直道上做匀变速直线运动,在弯道上做匀速圆周运动,重力加速度g=10m/s2,要使赛车绕赛道一周用时最短,下列说法正确的是( )| A. | 在小圆弧弯道上的速率为15$\sqrt{3}$m/s | B. | 在大圆弧弯道上的速率为30$\sqrt{3}$m/s | ||
| C. | 在直道上的加速度大小为$\frac{15\sqrt{3}}{4}$m/s2 | D. | 通过大圆弧弯道的时间为$\frac{4π\sqrt{6}}{3}$s |
分析 根据牛顿第二定律,结合最大静摩擦力提供向心力求出在两个弯道上的最大速度.
赛车在绕过小弯道后加速,根据几何关系求出直道的距离,结合速度位移公式求出加速度.
根据几何关系求出大圆弧的长度,结合运动学公式求出在圆弧上的运动时间.
解答 解:A、在弯道上做匀速圆周运动时,根据牛顿定律有:kmg=$m\frac{{{v}_{m}}^{2}}{r}$,
在小弯道上的最大速度为:${v}_{mr}=\sqrt{kgr}=\sqrt{2.25×10×30}$m/s=$15\sqrt{3}$m/s,故A正确;
B、在大圆弧弯道上的速率为:${v}_{mR}=\sqrt{kgR}$=$\sqrt{2.25×10×60}m/s=15\sqrt{6}m/s$.故B错误;
C、当弯道半径一定 时,在弯道上的最大速度是一定的,且在大弯道上的最大速度大于小弯道上的最大速度,故要想时间最短,故可在绕过小圆弧弯道后加速,直道的长度为:$x=\sqrt{{L}^{2}-{(R-r)}^{2}}=\sqrt{6{0}^{2}-(60-30)^{2}}=30\sqrt{3}$m,
故在在直道上的加速度大小为为:$a=\frac{{v}_{mR}^{2}-{v}_{mr}^{2}}{2x}$=$\frac{1350-675}{2×30\sqrt{3}}$=$\frac{15\sqrt{3}}{4}$m/s2,
D、通过大圆弧时间为:${t}_{2}=\frac{\frac{4πR}{3}}{{v}_{mR}}$,代入数据解得:t2=$\frac{8π\sqrt{6}}{9}$s.故D错误.
故选:AC
点评 解答此题的关键是由题目获得条件:①在弯道上由最大静摩擦力提供向心力②由数学知识求得圆弧的长度,另外还要熟练掌握匀速圆周运动的知识.

 名校课堂系列答案
名校课堂系列答案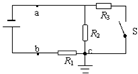 如图所示电路,R1、R2、R3是定值电阻,c点接地,a、b两接线柱接上直流电源,开关S是断开的,那么,当开关S闭合后( )
如图所示电路,R1、R2、R3是定值电阻,c点接地,a、b两接线柱接上直流电源,开关S是断开的,那么,当开关S闭合后( )| A. | ab两点电势均升高 | B. | ab两点电势均降低 | ||
| C. | a点电势升高,b点电势降低 | D. | a点电势降低,b点电势升高 |
 如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面间的电势差相等,实线为一带正电的质点仅在电场力作用下的运动轨迹,P、Q是这条轨迹上的两点,据此可知( )
如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面间的电势差相等,实线为一带正电的质点仅在电场力作用下的运动轨迹,P、Q是这条轨迹上的两点,据此可知( )| A. | 三个等势面中,c的电势较高 | B. | 带电质点通过Q点时的电势能较大 | ||
| C. | 带电质点通过P点时的动能较大 | D. | 带电质点通过Q点时的加速度较大 |
 用细线将小球悬挂在O点,O点的正下方有一光滑的钉子P,把小球拉到与钉子P等高的位置,摆线被钉子挡住,如图所示,让小球从静止释放后向右摆动,当小球第一次经过最低点时(线没有断),则( )
用细线将小球悬挂在O点,O点的正下方有一光滑的钉子P,把小球拉到与钉子P等高的位置,摆线被钉子挡住,如图所示,让小球从静止释放后向右摆动,当小球第一次经过最低点时(线没有断),则( )| A. | 小球的角速度不变 | B. | 小球的线速度不变 | ||
| C. | 小球的向心加速度增大 | D. | 悬线的拉力变大 |
 如图所示,质量为m的物体,在水平外力F作用下,以速度v沿水平面匀速运动,当物体运动到A点时撤去外力F,物体由A点继续向前滑行的过程中经过B点,则物体由A点到B点的过程中,下列说法正确的是( )
如图所示,质量为m的物体,在水平外力F作用下,以速度v沿水平面匀速运动,当物体运动到A点时撤去外力F,物体由A点继续向前滑行的过程中经过B点,则物体由A点到B点的过程中,下列说法正确的是( )| A. | v越大,摩擦力对物体的冲量越大;摩擦力做功越多 | |
| B. | v越大,摩擦力对物体的冲量越大;摩擦力做功与v的大小无关 | |
| C. | v越大,摩擦力对物体的冲量越小;摩擦力做功越少 | |
| D. | v越大,摩擦力对物体的冲量越小;摩擦力做功与v的大小无关 |
| A. | 7点20分 | B. | 11点50分 | C. | 40分钟 | D. | 2点30分 |
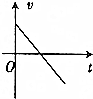
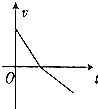
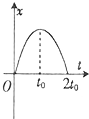
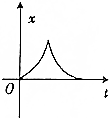
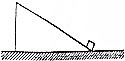 如图所示,一滑块以初速度v0从固定的粗糙斜面底端上滑,若用x,v,t分别表示滑块的位移、速度和滑行时间,则下列四幅图中能反映滑块从斜面底端出发到返回到斜面底端的是( )
如图所示,一滑块以初速度v0从固定的粗糙斜面底端上滑,若用x,v,t分别表示滑块的位移、速度和滑行时间,则下列四幅图中能反映滑块从斜面底端出发到返回到斜面底端的是( )