��Ŀ����
����Ŀ����ͼ��ʾ����Ǧ�=30���б����C������ˮƽ���ϣ�����Ϊm��С�������б�����ϵĺ��������£���A���ɾ�ֹ��ʼ�˶��������б���Ķ�Ħ��������= ![]() ���������ٶ�Ϊg��
���������ٶ�Ϊg��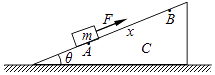
��1����б���屣�־�ֹ��tʱ���������A�˶���B������B��ʱ�ٶ�Ϊv���������ٶ�a�Ĵ�С������F�Ĵ�С��
��2���ڣ�1������£�����˶������У���б�����ܵ�ˮƽ���Ħ������
��3����ˮƽ��⻬��С����ڴ�СΪF=mg����б�����ϵĺ��������£���б����C������Ծ�ֹһ�������˶�������������Ի������ƣ���б���������M��
���𰸡�
��1���⣺���ݼ��ٶȵĶ���ʽ�ɵü��ٶȴ�СΪ��a= ![]() ��
��
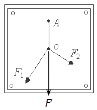
������Ϊ�о���������������ͼ��ʾ��
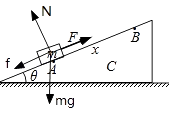
����ţ�ٵڶ����ɿɵã�F��mgsin30�㩁��mgcos30��=ma��
��ã�F=mg+ ![]() ��
��
�������ٶȵĴ�СΪ ![]() ������F�Ĵ�СΪmg+
������F�Ĵ�СΪmg+ ![]() ��
��
��2���⣺��б��Ϊ�о������������������ͼ��ʾ��
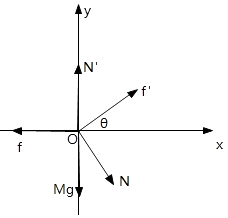
ˮƽ������ݹ�������ƽ�������ɵõ����б���Ħ����Ϊ��
f=Nsin��+f��cos��=mgcos��sin��+��mgcos��sin��= ![]() ��
��
��������
���ڣ�1������£�����˶������У�б�����ܵ�ˮƽ���Ħ����Ϊ ![]() ����������
����������
��3���⣺��mΪ�о�������ˮƽ�������ţ�ٵڶ����ɿɵã�Fcos30�㩁Nsin30��=ma��
����ֱ����Fsin30��+Ncos30��=mg��
������Ϊ�о�����ˮƽ�������ţ�ٵڶ����ɿɵã�Fcos30��=��M+m��a��
������ã�M= ![]() ��
��
����ˮƽ��⻬��С����ڴ�СΪF=mg����б�����ϵĺ��������£���б����C������Ծ�ֹһ�������˶�������������Ի������ƣ�б���������Ϊ ![]() ��
��
����������1�����ݼ��ٶȵĶ���ʽ�ɵü��ٶȴ�С��������Ϊ�о�������ţ�ٵڶ����ɿɵú���F��С����2����б��Ϊ�о������������������ˮƽ������ݹ�������ƽ�������ɵõ����б���Ħ��������3����mΪ�о�������ˮƽ�������ֱ�������ţ�ٵڶ������з��̣���������Ϊ�о�����ˮƽ�������ţ�ٵڶ������з���������⣮

 һ����ʦ�����Ծ�ϵ�д�
һ����ʦ�����Ծ�ϵ�д� �����Ծ���Ԫ���Ծ�ϵ�д�
�����Ծ���Ԫ���Ծ�ϵ�д�