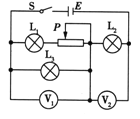
题目内容
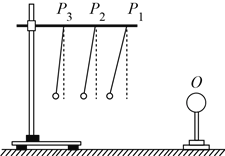
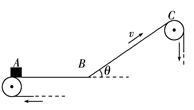
【题目】如图，一不可伸长的轻绳上端悬挂于O点，下端系一质量m=1.0 kg的小球。现将小球拉到A点（保持绳绷直）由静止释放，当它经过B点时绳恰好被拉断，小球平抛后落到水平地面上的C点，地面上的D点与OB在同一竖直线上，已知绳长L=1.0 m，B点离地高度H=1.0 m，A、B两点的高度差h=0.5 m，重力加速度
，不计空气影响，求：
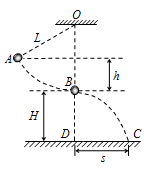
（1）地面上DC两点间的距离s；
（2）在B点轻绳所受的最大拉力大小。
【答案】（1）
（2）F=20 N
【解析】（1）设小球在B点速度为v，对小球从A到B由动能定理得：
①
绳子断后，小球做平抛运动，运动时间为t，则有：
②
DC间距离：
解得：
（2）在B位置，设绳子最大力量为F，由牛顿第二定律得：
④
联立①④得：F=2mg=2×1×10 N=20 N
根据牛顿第三定律，有F'=F，因而轻绳所受的最大拉力为20 N
【题目】某同学利用如图所示实验装置“探究加速度与力、质量的关系”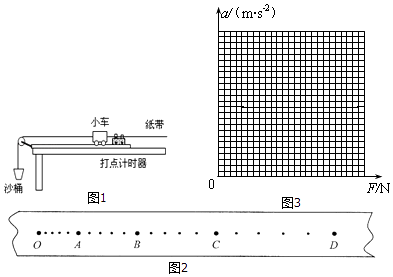
（1）实验中打点计时器应接电源（选填“交流”或“直流”）；为了用沙和沙桶的重力表示绳上拉力，实验中小车质量应沙和沙桶的总质量．（选填“远大于”、“远小于”或“等于”）
（2）该同学实验中打出了一条纸带，如图2所示，计时器打点的时间间隔为0.02s，从比较清晰的点起，每5个点取1个计数点，量出相邻两个计数点之间的距离分别为：OA=1.40cm，AB=1.70cm，BC=2.00cm，CD=2.30cm，由此可知，小车的加速度大小为m/s2 ．
（3）在实验中保持小车质量不变，改变沙和沙桶的总质量，测的沙和沙桶的总重力F和加速度a的数据如表：
①根据测得的数据，在图3中作出a=F图象；
F/N | 0.21 | 0.30 | 0.40 | 0.49 | 0.60 |
a/（ms﹣2） | 0.10 | 0.21 | 0.29 | 0.41 | 0.49 |
②由图象可知，小车与长木板之间的最大静摩擦力大小为N（结果保留两位有效数字）．
