题目内容
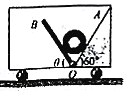
【题目】如图所示,光滑斜面的倾角α=30°,在斜面上放置一矩形线框abcd,ab边的边长l1=1 m,bc边的边长l2=0.6 m,线框的质量m=1 kg,电阻R=0.1 Ω,线框通过细线与重物相连,重物质量M=2 kg,斜面上ef(ef∥gh)的右方有垂直斜面向上的匀强磁场,磁感应强度B=0.5 T,如果线框从静止开始运动,进入磁场的最初一段时间做匀速运动,ef和gh的距离x=11.4 m,(取g=10 m/s2),求:

(1)线框进入磁场前重物的加速度;
(2)线框进入磁场时匀速运动的速度v.
【答案】(1)a=5 m/s2 (2) v=6m/s
【解析】(1)线框进入磁场前,仅受细线的拉力F,斜面的支持力和线框的重力的作用,重物受自身的重力和细线的拉力F′的作用。对线框由牛顿第二定律得F-mgsin α=ma
对重物由牛顿第二定律得Mg-F′=Ma
又F=F′
联立解得线框进入磁场前重物的加速度a=![]() =5 m/s2
=5 m/s2
(2)因为线框进入磁场的最初一段时间做匀速运动,则重物受力平衡:Mg=F1
线框abcd受力平衡:F1=mgsin α+F安
ab边进入磁场切割磁感线,产生的感应电动势E=Bl1v
回路中的感应电流为![]() ,ab边受到的安培力为F安=BIl1
,ab边受到的安培力为F安=BIl1
联立解得Mg=mgsin α+![]()
代入数据解得v=6 m/s。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目