题目内容
7.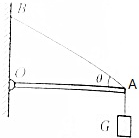 如图所示,一轻质横杆0端用铰链固定于墙上,A端用轻绳拉紧使0A杆保持水平.若在A端挂一重物G,在把重物的悬点从A向O缓慢移动的过程中,下列判断中正确的是( )
如图所示,一轻质横杆0端用铰链固定于墙上,A端用轻绳拉紧使0A杆保持水平.若在A端挂一重物G,在把重物的悬点从A向O缓慢移动的过程中,下列判断中正确的是( )| A. | 墙对杆的作用力一直变大 | B. | 墙对杆的作用力先变小,后变大 | ||
| C. | 墙对杆的作用力先变大,后变小 | D. | 墙对杆的作用力的最小值为Gcosθ |
分析 轻质横杆重力不计,分析横杆的受力情况,由杠杆平衡条件分析AB绳子张力的变化,再运用正交分解法列式分析墙对杆作用力的变化.
解答 解:设重物的悬点到O点的距离为S.AO长度为L.墙对杆的作用力为F,方向与水平方向的夹角为α.AB绳的张力为T.
以O支点,由杠杆平衡条件得:GS=TLsinθ,得 T=$\frac{GS}{Lsinθ}$,在把重物的悬点从A向O缓慢移动的过程中S减小时,则T减小.
对横杆OB,由正交分解法可得:
竖直方向上有:Fsinα+Tsinθ=G
水平方向上有:Fcosα=Tcosθ
解得 F=G$\sqrt{1-\frac{2S}{L}+\frac{{S}^{2}}{{L}^{2}si{n}^{2}θ}}$
根据数学知识可知,F先变小,后变大.当满足:S=-$\frac{b}{2a}$=-$\frac{\frac{2}{L}}{2×\frac{1}{{L}^{2}sinθ}}$=Lsinθ时F有最小值,最小值为 Fmin=G$\sqrt{2-2sinθ}$
故选:B
点评 本题是力矩平衡和共点力平衡条件的综合应用,运用函数法求解极值,关键要熟练运用正交分解法列式.

练习册系列答案
相关题目
18.一辆汽车以30m/s的速度沿平直路面行驶,当汽车以5m/s2的加速度刹车 时,则刹车4s内与刹车8s内的位移之比为( )
| A. | 1:1 | B. | 8:9 | C. | 3:1 | D. | 9:8 |
15.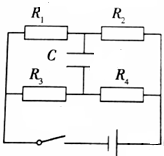 在图示电路中,R1=100Ω,R2=200Ω,R3=80Ω,C=20μF,电源电动势为12V,电源内阻不计,闭合电键后,若要使电容器所带电荷量为4×10-5C,则R4的阻值应为( )
在图示电路中,R1=100Ω,R2=200Ω,R3=80Ω,C=20μF,电源电动势为12V,电源内阻不计,闭合电键后,若要使电容器所带电荷量为4×10-5C,则R4的阻值应为( )
 在图示电路中,R1=100Ω,R2=200Ω,R3=80Ω,C=20μF,电源电动势为12V,电源内阻不计,闭合电键后,若要使电容器所带电荷量为4×10-5C,则R4的阻值应为( )
在图示电路中,R1=100Ω,R2=200Ω,R3=80Ω,C=20μF,电源电动势为12V,电源内阻不计,闭合电键后,若要使电容器所带电荷量为4×10-5C,则R4的阻值应为( )| A. | 40Ω | B. | 80Ω | C. | 160Ω | D. | 400Ω |
12.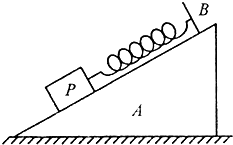 如图所示,斜面体A放置再水平地面上,物块P放在斜面上,用平行于斜面的轻弹簧将物块P栓接在挡板B上,在物块P上施加竖直向上的拉力F,整个系统处于静止状态,下列作用力一定存在的是( )
如图所示,斜面体A放置再水平地面上,物块P放在斜面上,用平行于斜面的轻弹簧将物块P栓接在挡板B上,在物块P上施加竖直向上的拉力F,整个系统处于静止状态,下列作用力一定存在的是( )
 如图所示,斜面体A放置再水平地面上,物块P放在斜面上,用平行于斜面的轻弹簧将物块P栓接在挡板B上,在物块P上施加竖直向上的拉力F,整个系统处于静止状态,下列作用力一定存在的是( )
如图所示,斜面体A放置再水平地面上,物块P放在斜面上,用平行于斜面的轻弹簧将物块P栓接在挡板B上,在物块P上施加竖直向上的拉力F,整个系统处于静止状态,下列作用力一定存在的是( )| A. | 物块P与斜面之间的摩擦力 | B. | 物块P与斜面之间的弹力 | ||
| C. | 地面与斜面体A之间的摩擦力 | D. | 地面与斜面体A之间的弹力 |
7. xOy平面内以O为圆心的圆形区域内有一方向垂直xOy平面的匀强磁场.一个质量为m、电荷量为q的带电粒子由原点O开始运动,初速度为v,方向沿x轴正方向.后来,粒子经过y轴上的P点,如图所示.不计重力的影响,粒子经过P点时的速度方向可能是( )
xOy平面内以O为圆心的圆形区域内有一方向垂直xOy平面的匀强磁场.一个质量为m、电荷量为q的带电粒子由原点O开始运动,初速度为v,方向沿x轴正方向.后来,粒子经过y轴上的P点,如图所示.不计重力的影响,粒子经过P点时的速度方向可能是( )
 xOy平面内以O为圆心的圆形区域内有一方向垂直xOy平面的匀强磁场.一个质量为m、电荷量为q的带电粒子由原点O开始运动,初速度为v,方向沿x轴正方向.后来,粒子经过y轴上的P点,如图所示.不计重力的影响,粒子经过P点时的速度方向可能是( )
xOy平面内以O为圆心的圆形区域内有一方向垂直xOy平面的匀强磁场.一个质量为m、电荷量为q的带电粒子由原点O开始运动,初速度为v,方向沿x轴正方向.后来,粒子经过y轴上的P点,如图所示.不计重力的影响,粒子经过P点时的速度方向可能是( )| A. | 箭头a | B. | 箭头b | C. | 箭头c | D. | 箭头d |
5. 竖直向上放置的U形管,一端贮有一定质量的理想气体,另一端开口,在温度保持不变的情况下,设想沿CD将右管的上部分截去,则管中封闭的气体体积V和压强p的变化是( )
竖直向上放置的U形管,一端贮有一定质量的理想气体,另一端开口,在温度保持不变的情况下,设想沿CD将右管的上部分截去,则管中封闭的气体体积V和压强p的变化是( )
 竖直向上放置的U形管,一端贮有一定质量的理想气体,另一端开口,在温度保持不变的情况下,设想沿CD将右管的上部分截去,则管中封闭的气体体积V和压强p的变化是( )
竖直向上放置的U形管,一端贮有一定质量的理想气体,另一端开口,在温度保持不变的情况下,设想沿CD将右管的上部分截去,则管中封闭的气体体积V和压强p的变化是( )| A. | 体积V和压强p均增大 | B. | 体积V和压强p均减小 | ||
| C. | 体积V增大,压强p减小 | D. | 体积V减小,压强p增大 |
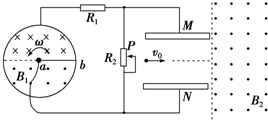 如图所示,半径为L1=2m的金属圆环内上、下半圆各有垂直圆环平面的有界匀强磁场,磁感应强度大小均为B1=$\frac{10}{π}$ T.长度也为L1、电阻为R的金属杆ab,一端处于圆环中心,另一端恰好搭接在金属环上,绕着a端沿逆时针方向匀速转动,角速度为ω=$\frac{π}{10}$ rad/s.通过导线将金属杆的a端和金属环连接到图示的电路中(连接a端的导线与圆环不接触,图中的定值电阻R1=R,滑片P位于R2的正中央,R2的总阻值为4R),图中的平行板长度为L2=2m,宽度为d=2m.图示位置为计时起点,在平行板左边缘中央处刚好有一带电粒子以初速度v0=0.5m/s向右运动,并恰好能从平行板的右边缘飞出,之后进入到有界匀强磁场中,其磁感应强度大小为B2,左边界为图中的虚线位置,右侧及上下范围均足够大.(忽略金属杆与圆环的接触电阻、圆环电阻及导线电阻,忽略电容器的充放电时间,忽略带电粒子在磁场中运动时的电磁辐射的影响,不计平行金属板两端的边缘效应及带电粒子的重力和空气阻力)求:
如图所示,半径为L1=2m的金属圆环内上、下半圆各有垂直圆环平面的有界匀强磁场,磁感应强度大小均为B1=$\frac{10}{π}$ T.长度也为L1、电阻为R的金属杆ab,一端处于圆环中心,另一端恰好搭接在金属环上,绕着a端沿逆时针方向匀速转动,角速度为ω=$\frac{π}{10}$ rad/s.通过导线将金属杆的a端和金属环连接到图示的电路中(连接a端的导线与圆环不接触,图中的定值电阻R1=R,滑片P位于R2的正中央,R2的总阻值为4R),图中的平行板长度为L2=2m,宽度为d=2m.图示位置为计时起点,在平行板左边缘中央处刚好有一带电粒子以初速度v0=0.5m/s向右运动,并恰好能从平行板的右边缘飞出,之后进入到有界匀强磁场中,其磁感应强度大小为B2,左边界为图中的虚线位置,右侧及上下范围均足够大.(忽略金属杆与圆环的接触电阻、圆环电阻及导线电阻,忽略电容器的充放电时间,忽略带电粒子在磁场中运动时的电磁辐射的影响,不计平行金属板两端的边缘效应及带电粒子的重力和空气阻力)求: