题目内容
如图所示，如果把水星和金星绕太阳的运动视为匀速圆周运动，从水星与金星在一条直线上开始计时，若天文学家测得在相同时间内水星转过的角度为θ1，金星转过的角度为θ2(θ1、θ2均为锐角)，则由此条件可求得（ ）
| A．水星和金星绕太阳运动的周期之比 |
| B．水星和金星的密度之比 |
| C．水星和金星到太阳中心的距离之比 |
| D．水星和金星绕太阳运动的向心加速度大小之比 |
ACD
解析试题分析：星球运动的周期为：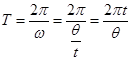
，可见周期之比等于
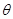角的反比，A正确；只能求得中心星的质量，B错误；由万有引力提供向心力得
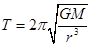,由周期之比可以求得环绕半径之比，即可以得到水星和金星到太阳中心的距离之比，C正确；星球绕太阳运动的向心加速度为
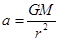，由半径之比可以求得加速度之比，D正确。
考点：本题考查了万有引力定律和圆周运动的规律
阅读快车系列答案如图所示，三颗质量均为m的地球同步卫星等间隔分布在半径为r的圆轨道上，设地球质量为M、半径为R.下列说法正确的是( )
A．地球对一颗卫星的引力大小为 |
B．一颗卫星对地球的引力大小为 |
C．两颗卫星之间的引力大小为 |
D．三颗卫星对地球引力的合力大小为 |
有些卫星因能量耗尽而报废，成为太空垃圾，所以被称为“垃圾卫星”。“轨道康复者”是“垃圾卫星”的救星，被称为“太空110”，它可在太空中给“垃圾卫星”补充能量，延长卫星的使用寿命。假设“轨道康复者”绕地球做匀速圆周运动时的轨道半径为地球同步卫星轨道半径的五分之一，其运动方向与地球自转方向一致，轨道平面与地球赤道平面重合。下列判断正确的是 （）
| A．“轨道康复者”的加速度是地球同步卫星加速度的25倍 |
B．“轨道康复者”的周期是地球同步卫星周期的 倍 |
| C．站在赤道上的人用仪器观察到“轨道康复者”向东运动 |
| D．“轨道康复者”要在原轨道上加速才能“拯救”更低轨道上的卫星 |
2013年12月2日1时30分，“嫦娥三号”月球探测器搭载长征三号乙火箭发射升空。该卫星将在距月球表面高度为h的轨道上做匀速圆周运动，其运行的周期为T；最终在月球表面实现软着陆。若以R表示月球的半径，忽略月球自转及地球对卫星的影响。则
A．“嫦娥三号”绕月运行时的向心加速度为 |
B．月球的第一宇宙速度为 |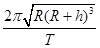
| C．“嫦娥三号”降落月球时，通常使用降落伞减速从而实现软着陆 |
D．物体在月球表面自由下落的加速度大小为 |
已知地球质量是月球质量的a倍，地球半径是月球半径的b倍，下列结论中正确的是( )
A．地球表面和月球表面的重力加速度之比为 |
B．环绕地球表面和月球表面运行卫星的速率之比为 |
C．环绕地球表面和月球表面运行卫星的周期之比为 |
D．环绕地球表面和月球表面运行卫星的角速度之比为 |
1970年4月24日，我国自行设计、制造的第一颗人造地球卫星“东方红一号”发射成功，开创了我国航天事业的新纪元．“东方红一号”的运行轨道为椭圆轨道，其近地点M和远地点N的高度分别为439km和2384km，则 （ ）
| A．卫星在N点的速度小于7．9km/s |
| B．卫星在N点的速度大于7．9km/s |
| C．卫星在M点的加速度大于N点的加速度 |
| D．卫星在N点若再适当加速则可进入过N点的圆轨道运行 |
牛顿以天体之间普遍存在着引力为依据，运用严密的逻辑推理，建立了万有引力定律。关于万有引力定律的创建，下列说法错误的是（ ）
| A．牛顿接受了胡克等科学家关于“吸引力与两中心距离的平方成反比”的猜想 |
| B．牛顿根据地球上一切物体都以相同加速度下落的事实，得出物体受地球的引力与其质量成正比，即Fµm的结论 |
| C．牛顿根据Fµm和牛顿第三定律，分析了地月间的引力关系，进而得出Fµm1m2 |
| D．牛顿根据大量实验数据得出了比例系数G的大小 |