题目内容
2.水的折射率为n,距水面深h处有一个点光源,岸上的人看到水面被该光源照亮的圆形区域的直径为( )| A. | 2htan(arc sin$\frac{1}{n}$) | B. | 2htan(arc sin n) | C. | 2htan(arc cos$\frac{1}{n}$) | D. | 2hcot(arc cos n) |
分析 水下点光源是向四面八方照射,当从水中射向空气时,若入射角大于或等于临界角,就会发生光的全反射.所以有区域的光不会射出.
解答 解:水下点光源射向空气时,当照射越远时入射角越大,照射越近则入射角越小.
由水的折射率n可求出水的临界角sinC=$\frac{1}{n}$ 则C=arcsin$\frac{1}{n}$
当入射角i等于C时,恰好发生全反射.
设上的人看到水面被该光源照亮的圆形区域的直径为D
则sini=$\frac{\frac{D}{2}}{\sqrt{{h}^{2}+(\frac{D}{2})^{2}}}$,因为 i=r 所以 sini=sinC
因此由$\frac{\frac{D}{2}}{\sqrt{{h}^{2}+(\frac{D}{2})^{2}}}$=$\frac{1}{n}$ 得D=$\sqrt{\frac{4{h}^{2}}{{n}^{2}-1}}$
或者也可以这样算:
恰好发生光的全反射时,则有
$\frac{\frac{D}{2}}{h}=tani$
所以D=2htani=2htan(arcsin$\frac{1}{n}$)
故选:A
点评 运用恰好发生全反射来确定光斑区域的大小,同时运用三角函数关系.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
12.据每日邮报2014年4月18日报道,美国国家航空航天局(NASA)目前宣布首次在太阳系外发现“类地”行星Kepler-186f.假如宇航员乘坐宇宙飞船到达该行星,进行科学观测:该行星自转周期为T;宇航员在该行星“北极”距该行星地面附近h处自由释放-个小球(引力视为恒力),落地时间为t1;宇航员在该行星“赤道”距该行星地面附近h处自由释放-个小球(引力视为恒力),落地时间为t2.则行星的半径R的值( )
| A. | R=$\frac{({{t}_{2}}^{2}+{{t}_{1}}^{2})h{T}^{2}}{4{π}^{2}{{t}_{1}}^{2}{{t}_{2}}^{2}}$ | |
| B. | R=$\frac{({{t}_{2}}^{2}+{{t}_{1}}^{2})h{T}^{2}}{2{π}^{2}{{t}_{1}}^{2}{{t}_{2}}^{2}}$ | |
| C. | R=$\frac{({{t}_{2}}^{2}-{{t}_{1}}^{2})h{T}^{2}}{2{π}^{2}{{t}_{1}}^{2}{{t}_{2}}^{2}}$ | |
| D. | R=$\frac{({{t}_{2}}^{2}-{{t}_{1}}^{2})h{T}^{2}}{4{π}^{2}{{t}_{1}}^{2}{{t}_{2}}^{2}}$ |
17. 如图所示.倾角为θ的固定斜面上有一质量为m的物体.在水平推力F的作用下沿斜面以速度v匀速向上移动了距离S.如果物体与斜面间的动摩擦因数为μ,则( )
如图所示.倾角为θ的固定斜面上有一质量为m的物体.在水平推力F的作用下沿斜面以速度v匀速向上移动了距离S.如果物体与斜面间的动摩擦因数为μ,则( )
 如图所示.倾角为θ的固定斜面上有一质量为m的物体.在水平推力F的作用下沿斜面以速度v匀速向上移动了距离S.如果物体与斜面间的动摩擦因数为μ,则( )
如图所示.倾角为θ的固定斜面上有一质量为m的物体.在水平推力F的作用下沿斜面以速度v匀速向上移动了距离S.如果物体与斜面间的动摩擦因数为μ,则( )| A. | 力F所做的功FSsinθ | |
| B. | 斜面体对物体做的功为mgSsinθ-FScosθ | |
| C. | 物体摩擦力所做的功为μ(mgcosθ-Fsinθ)S | |
| D. | 物体的重力做功为mgS |
7.下列关于匀速圆周运动的向心加速度的说法中正确的是( )
| A. | 向心加速度越大,物体速率变化越快 | |
| B. | 向心加速度越大,物体速度方向变化越快 | |
| C. | 在匀速圆周运动中,向心加速度是恒定的 | |
| D. | 向心加速度的方向始终与速度方向垂直 |
14.如图所示,a、b是绕太阳做圆轨道运动的2颗行星,下列说法正确的是( )


| A. | 行星a的线速度较小 | B. | 行星a的角速度较小 | ||
| C. | 行星a的周期较短 | D. | 行星a的向心加速度较小 |
12. 如图所示,在xOy平面内,有一个圆形区域的直径AB与x轴重合,圆心O′的坐标为(2a,0),其半径为a,该区域内无磁场.在y轴和直线x=3a之间的其他区域内存在垂直纸面向外的匀强磁场,磁感应强度大小为B.一质量为m、电荷量为q的带正电的粒子从y轴上某点射入磁场.不计粒子重力.则( )
如图所示,在xOy平面内,有一个圆形区域的直径AB与x轴重合,圆心O′的坐标为(2a,0),其半径为a,该区域内无磁场.在y轴和直线x=3a之间的其他区域内存在垂直纸面向外的匀强磁场,磁感应强度大小为B.一质量为m、电荷量为q的带正电的粒子从y轴上某点射入磁场.不计粒子重力.则( )
 如图所示,在xOy平面内,有一个圆形区域的直径AB与x轴重合,圆心O′的坐标为(2a,0),其半径为a,该区域内无磁场.在y轴和直线x=3a之间的其他区域内存在垂直纸面向外的匀强磁场,磁感应强度大小为B.一质量为m、电荷量为q的带正电的粒子从y轴上某点射入磁场.不计粒子重力.则( )
如图所示,在xOy平面内,有一个圆形区域的直径AB与x轴重合,圆心O′的坐标为(2a,0),其半径为a,该区域内无磁场.在y轴和直线x=3a之间的其他区域内存在垂直纸面向外的匀强磁场,磁感应强度大小为B.一质量为m、电荷量为q的带正电的粒子从y轴上某点射入磁场.不计粒子重力.则( )| A. | 若粒子的初速度方向与y轴正向的夹角为60°,且粒子不经过圆形区域就能到达B点,粒子的初速度大小为$\frac{2qBa}{m}$ | |
| B. | 若粒子的初速度方向与y轴正向的夹角为60°,且粒子不经过圆形区域就能到达B点,粒子的初速度大小为$\frac{3qBa}{m}$ | |
| C. | 若粒子的初速度方向与y轴正向的夹角为60°,在磁场中运动的时间为△t=$\frac{πm}{3Bq}$,且粒子也能到达B点,粒子的初速度大小为$\frac{3qBa}{2m}$ | |
| D. | 若粒子的初速度方向与y轴正向的夹角为60°,在磁场中运动的时间为△t=$\frac{πm}{3Bq}$,且粒子也能到达B点,粒子的初速度大小为$\frac{\sqrt{3}qBa}{2m}$ |
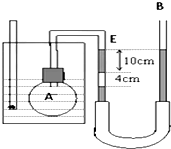 如图所示为验证查理定律的实验装置.A为烧瓶,内贮空气.B为U形管,下部与较长的软橡胶管相连.由于组装不慎,U形管左侧10cm水银柱的下方混入一段长为4cm的空气柱,左侧水银柱上表面与标志线E对齐.开始时烧瓶所在水槽内水温为7℃,U形管两边水银面相平.当水温升至63℃时,调整右边开口水银管的高度,使左侧水银柱上表面仍与标志线E对齐.已知大气压p0=76cmHg.此时:
如图所示为验证查理定律的实验装置.A为烧瓶,内贮空气.B为U形管,下部与较长的软橡胶管相连.由于组装不慎,U形管左侧10cm水银柱的下方混入一段长为4cm的空气柱,左侧水银柱上表面与标志线E对齐.开始时烧瓶所在水槽内水温为7℃,U形管两边水银面相平.当水温升至63℃时,调整右边开口水银管的高度,使左侧水银柱上表面仍与标志线E对齐.已知大气压p0=76cmHg.此时: 如图所示,在光滑的水平面上,有A、B、C三个物体,C的左端与弹簧相连,弹簧处于原长.已知A B C三个物体的质量均为4kg,其中物体B和C处于静止状态,A以V0=6m/s的速度向右运动,与物体B碰撞后粘在一起继续向右运动,求:
如图所示,在光滑的水平面上,有A、B、C三个物体,C的左端与弹簧相连,弹簧处于原长.已知A B C三个物体的质量均为4kg,其中物体B和C处于静止状态,A以V0=6m/s的速度向右运动,与物体B碰撞后粘在一起继续向右运动,求: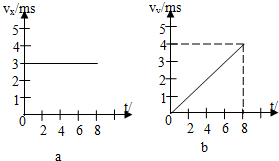 如图所示,α图表示某物体在x轴方向上分速度的v-t图象,b图表示该物体在y轴上分速度图象.
如图所示,α图表示某物体在x轴方向上分速度的v-t图象,b图表示该物体在y轴上分速度图象.