题目内容
12.据每日邮报2014年4月18日报道,美国国家航空航天局(NASA)目前宣布首次在太阳系外发现“类地”行星Kepler-186f.假如宇航员乘坐宇宙飞船到达该行星,进行科学观测:该行星自转周期为T;宇航员在该行星“北极”距该行星地面附近h处自由释放-个小球(引力视为恒力),落地时间为t1;宇航员在该行星“赤道”距该行星地面附近h处自由释放-个小球(引力视为恒力),落地时间为t2.则行星的半径R的值( )| A. | R=$\frac{({{t}_{2}}^{2}+{{t}_{1}}^{2})h{T}^{2}}{4{π}^{2}{{t}_{1}}^{2}{{t}_{2}}^{2}}$ | |
| B. | R=$\frac{({{t}_{2}}^{2}+{{t}_{1}}^{2})h{T}^{2}}{2{π}^{2}{{t}_{1}}^{2}{{t}_{2}}^{2}}$ | |
| C. | R=$\frac{({{t}_{2}}^{2}-{{t}_{1}}^{2})h{T}^{2}}{2{π}^{2}{{t}_{1}}^{2}{{t}_{2}}^{2}}$ | |
| D. | R=$\frac{({{t}_{2}}^{2}-{{t}_{1}}^{2})h{T}^{2}}{4{π}^{2}{{t}_{1}}^{2}{{t}_{2}}^{2}}$ |
分析 根据自由落体运动的规律求出该行星地面附近的重力加速度;
在该行星“赤道”处物体做圆周运动需要的向心力等于万有引力与该位置重力之差列出等式求解;
解答 解:宇航员在该行星“北极”距该行星地面附近h处自由释放-个小球(引力视为恒力),落地时间为t1;
h=$\frac{1}{2}$g${t}_{1}^{2}$
g=$\frac{2h}{{t}_{1}^{2}}$
宇航员在该行星“赤道”距该行星地面附近h处自由释放-个小球(引力视为恒力),落地时间为t2.
h=$\frac{1}{2}$g′${t}_{2}^{2}$
g′=$\frac{2h}{{t}_{2}^{2}}$
在该行星“赤道”处物体做圆周运动需要的向心力等于万有引力与该位置重力之差列出等式
m$\frac{4{π}^{2}}{{T}^{2}}$R=mg-mg′
解得:R=$\frac{({{t}_{2}}^{2}-{{t}_{1}}^{2})h{T}^{2}}{2{π}^{2}{{t}_{1}}^{2}{{t}_{2}}^{2}}$
故选:C.
点评 本题关键是通过自由落体运动求出星球表面的重力加速度,再根据万有引力提供圆周运动向心力和万有引力等于重力求解.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
2.在电场和重力场都存在的空间中,一带电小球从A点运动到B点,电场力做了10J的功,重力做了6J的功,克服阻力做了7J的功,则此过程中带电小球的( )
| A. | 机械能增加了10J,动能增加了9J | |
| B. | 机械能增加了3J,动能增加了9J | |
| C. | 电势能增加了10J,动能增加了9J | |
| D. | 电势能减少了10J,重力势能增加了6J |
20. 如图所示,球与斜面光滑接触,用水平推力F缓慢推动斜面使球升到A端(此时绳子接近水平位置),在此过程中,绳子的拉力为T,球对斜面的压力为N,则( )
如图所示,球与斜面光滑接触,用水平推力F缓慢推动斜面使球升到A端(此时绳子接近水平位置),在此过程中,绳子的拉力为T,球对斜面的压力为N,则( )
 如图所示,球与斜面光滑接触,用水平推力F缓慢推动斜面使球升到A端(此时绳子接近水平位置),在此过程中,绳子的拉力为T,球对斜面的压力为N,则( )
如图所示,球与斜面光滑接触,用水平推力F缓慢推动斜面使球升到A端(此时绳子接近水平位置),在此过程中,绳子的拉力为T,球对斜面的压力为N,则( )| A. | N不断增大,T先减小后增大 | B. | N不断增大,T不断减小 | ||
| C. | N不变,T不断增大 | D. | N不变,T先减小后增大 |
7. 如图所示,人造卫星A、B在同一平面内绕地心O做匀速圆周运动.已知A、B连线与A、O连线间的夹角最大为θ,则卫星A、B的角速度之比$\frac{{ω}_{1}}{{ω}_{2}}$等于( )
如图所示,人造卫星A、B在同一平面内绕地心O做匀速圆周运动.已知A、B连线与A、O连线间的夹角最大为θ,则卫星A、B的角速度之比$\frac{{ω}_{1}}{{ω}_{2}}$等于( )
 如图所示,人造卫星A、B在同一平面内绕地心O做匀速圆周运动.已知A、B连线与A、O连线间的夹角最大为θ,则卫星A、B的角速度之比$\frac{{ω}_{1}}{{ω}_{2}}$等于( )
如图所示,人造卫星A、B在同一平面内绕地心O做匀速圆周运动.已知A、B连线与A、O连线间的夹角最大为θ,则卫星A、B的角速度之比$\frac{{ω}_{1}}{{ω}_{2}}$等于( )| A. | sin3θ | B. | $\frac{1}{si{n}^{3}θ}$ | C. | $\sqrt{si{n}^{3}θ}$ | D. | $\sqrt{\frac{1}{si{n}^{3}θ}}$ |
17. 如图是一探究功能关系的实验装置,水平面与斜面交于B点,轻弹簧左端固定于竖直墙面,用质量为m的滑块压缩弹簧至D点,由静止释放,滑块脱离弹簧后恰好能滑到斜面最高点C;然后,去掉斜面改用圆弧形轨道,让滑块由相同位置D静止释放,滑块沿圆弧轨道上升至某点.已知水平面、斜面BC、圆弧形轨道和滑块间的动摩擦因数均为μ,BD=L1,斜面底边BE=L2,倾角为θ.滑块可视为质点,不计滑块在B点的机械能损失,则( )
如图是一探究功能关系的实验装置,水平面与斜面交于B点,轻弹簧左端固定于竖直墙面,用质量为m的滑块压缩弹簧至D点,由静止释放,滑块脱离弹簧后恰好能滑到斜面最高点C;然后,去掉斜面改用圆弧形轨道,让滑块由相同位置D静止释放,滑块沿圆弧轨道上升至某点.已知水平面、斜面BC、圆弧形轨道和滑块间的动摩擦因数均为μ,BD=L1,斜面底边BE=L2,倾角为θ.滑块可视为质点,不计滑块在B点的机械能损失,则( )
 如图是一探究功能关系的实验装置,水平面与斜面交于B点,轻弹簧左端固定于竖直墙面,用质量为m的滑块压缩弹簧至D点,由静止释放,滑块脱离弹簧后恰好能滑到斜面最高点C;然后,去掉斜面改用圆弧形轨道,让滑块由相同位置D静止释放,滑块沿圆弧轨道上升至某点.已知水平面、斜面BC、圆弧形轨道和滑块间的动摩擦因数均为μ,BD=L1,斜面底边BE=L2,倾角为θ.滑块可视为质点,不计滑块在B点的机械能损失,则( )
如图是一探究功能关系的实验装置,水平面与斜面交于B点,轻弹簧左端固定于竖直墙面,用质量为m的滑块压缩弹簧至D点,由静止释放,滑块脱离弹簧后恰好能滑到斜面最高点C;然后,去掉斜面改用圆弧形轨道,让滑块由相同位置D静止释放,滑块沿圆弧轨道上升至某点.已知水平面、斜面BC、圆弧形轨道和滑块间的动摩擦因数均为μ,BD=L1,斜面底边BE=L2,倾角为θ.滑块可视为质点,不计滑块在B点的机械能损失,则( )| A. | 释放滑块前弹簧的弹性势能为μmg(L1+L2)+mgL2tanθ | |
| B. | 滑块由D点滑到B点时动能为μmgL2+mgL2tanθ | |
| C. | 在两次运动过程中滑块上升的高度相同 | |
| D. | 在两次运动过程中滑块的机械能损失均为μmg(L1+$\frac{{L}_{2}}{cosθ}$) |
2.水的折射率为n,距水面深h处有一个点光源,岸上的人看到水面被该光源照亮的圆形区域的直径为( )
| A. | 2htan(arc sin$\frac{1}{n}$) | B. | 2htan(arc sin n) | C. | 2htan(arc cos$\frac{1}{n}$) | D. | 2hcot(arc cos n) |
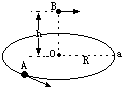 如图所示,小球A在光滑的半径为R的圆形槽内作匀速圆周运动,当它运动到图中的a点时,在圆形槽中心O点正上方h处,有一小球B沿0a方向以某一初速水平抛出,结果恰好在a点与A球相碰,g=10m/s2求
如图所示,小球A在光滑的半径为R的圆形槽内作匀速圆周运动,当它运动到图中的a点时,在圆形槽中心O点正上方h处,有一小球B沿0a方向以某一初速水平抛出,结果恰好在a点与A球相碰,g=10m/s2求 有一半圆柱玻璃砖,横截面如图所示,半径为R,O为圆心,一束平行光从左半侧AC面入射,O点左侧恰好无出射光线,已知玻璃砖的折射率为$\sqrt{2}$.求在OB段出射光束的宽度.
有一半圆柱玻璃砖,横截面如图所示,半径为R,O为圆心,一束平行光从左半侧AC面入射,O点左侧恰好无出射光线,已知玻璃砖的折射率为$\sqrt{2}$.求在OB段出射光束的宽度.