题目内容
10. 如图所示,在光滑的水平面上,有A、B、C三个物体,C的左端与弹簧相连,弹簧处于原长.已知A B C三个物体的质量均为4kg,其中物体B和C处于静止状态,A以V0=6m/s的速度向右运动,与物体B碰撞后粘在一起继续向右运动,求:
如图所示,在光滑的水平面上,有A、B、C三个物体,C的左端与弹簧相连,弹簧处于原长.已知A B C三个物体的质量均为4kg,其中物体B和C处于静止状态,A以V0=6m/s的速度向右运动,与物体B碰撞后粘在一起继续向右运动,求:(1)物体A与物体B碰撞时,物体B获得的速度大小以及损失的能量?
(2)物体A与物体B碰撞粘在一起,在以后的运动中,弹簧的弹性势能最大值?
分析 (1)A、B碰撞过程系统动量守恒,应用动量守恒定律可以求出碰撞后的速度,然后应用能量守恒定律可以求出损失的机械能.
(2)A、B、C三者组成的系统动量守恒,当三者速度相等时弹簧的压缩量最大弹簧的弹性势能最大,应用动量守恒定律求出共同速度,然后由能量守恒定律求出弹簧的最大弹性势能.
解答 解:(1)物体A、B组成的系统碰撞过程动量守恒,以向右为正方向,
由动量守恒定律得:mv0=(m+m)vAB,代入数据解得:vAB=3m/s,
由能量守恒定律得:E损=$\frac{1}{2}$mv02-$\frac{1}{2}$(m+m)vAB2,
代入数据解得:E损=36J;
(2)当A、B、C速度相等时,弹簧压缩量最大,弹簧弹性势能最大,
A、B、C组成的系统动量守恒,以向右为正方向,
由动量守恒定律得:mv0=(m+m+m)v共,代入数据解得:v共=2m/s,
由能量守恒定律得:$\frac{1}{2}$(m+m)vAB2=$\frac{1}{2}$(m+m+m)v共2+EP,
代入数据解得,弹簧的最大弹性势能:EP=12J;
答:(1)物体A与物体B碰撞时,物体B获得的速度大小为3m/s,损失的能量为36J.
(2)物体A与物体B碰撞粘在一起,在以后的运动中,弹簧的弹性势能最大值为12J.
点评 本题考查了求速度、弹性势能问题,分析清楚运动过程、应用动量守恒定律与能量守恒定律可以正确解题,分析清楚物体运动过程,合理选择研究对象与运动过程是正确解题的前提.

练习册系列答案
相关题目
20. 如图所示,球与斜面光滑接触,用水平推力F缓慢推动斜面使球升到A端(此时绳子接近水平位置),在此过程中,绳子的拉力为T,球对斜面的压力为N,则( )
如图所示,球与斜面光滑接触,用水平推力F缓慢推动斜面使球升到A端(此时绳子接近水平位置),在此过程中,绳子的拉力为T,球对斜面的压力为N,则( )
 如图所示,球与斜面光滑接触,用水平推力F缓慢推动斜面使球升到A端(此时绳子接近水平位置),在此过程中,绳子的拉力为T,球对斜面的压力为N,则( )
如图所示,球与斜面光滑接触,用水平推力F缓慢推动斜面使球升到A端(此时绳子接近水平位置),在此过程中,绳子的拉力为T,球对斜面的压力为N,则( )| A. | N不断增大,T先减小后增大 | B. | N不断增大,T不断减小 | ||
| C. | N不变,T不断增大 | D. | N不变,T先减小后增大 |
18.在如图甲所示的电路中,内阻不计的电源的电动势为3.0V,三只小灯泡的规格相同,该小灯泡的伏安特性曲线如图乙所示.当开关S闭合稳定后( )


| A. | 通过L1的电流大小为通过L2电流的2倍 | |
| B. | L1消耗的电功率为0.75W | |
| C. | L2消耗的电功率约为0.19W | |
| D. | L2的电阻为6Ω |
15.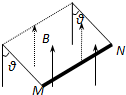 如图所示,金属棒MN两端由等长的轻质细线水平悬挂,处于竖直向上的匀强磁场中,棒中通以由M向N的电流,平衡时两悬线与竖直方向夹角均为θ.如果仅改变下列某一个条件,θ角的相应变化情况是( )
如图所示,金属棒MN两端由等长的轻质细线水平悬挂,处于竖直向上的匀强磁场中,棒中通以由M向N的电流,平衡时两悬线与竖直方向夹角均为θ.如果仅改变下列某一个条件,θ角的相应变化情况是( )
 如图所示,金属棒MN两端由等长的轻质细线水平悬挂,处于竖直向上的匀强磁场中,棒中通以由M向N的电流,平衡时两悬线与竖直方向夹角均为θ.如果仅改变下列某一个条件,θ角的相应变化情况是( )
如图所示,金属棒MN两端由等长的轻质细线水平悬挂,处于竖直向上的匀强磁场中,棒中通以由M向N的电流,平衡时两悬线与竖直方向夹角均为θ.如果仅改变下列某一个条件,θ角的相应变化情况是( )| A. | 棒中的电流变大,θ角变小 | B. | 两悬线等长变短,θ角变小 | ||
| C. | 金属棒质量变大,θ角变小 | D. | 磁感应强度变大,θ角变小 |
2.水的折射率为n,距水面深h处有一个点光源,岸上的人看到水面被该光源照亮的圆形区域的直径为( )
| A. | 2htan(arc sin$\frac{1}{n}$) | B. | 2htan(arc sin n) | C. | 2htan(arc cos$\frac{1}{n}$) | D. | 2hcot(arc cos n) |
19.关于功率,下列说法中正确的是( )
| A. | 力做功越多,其功率越大 | |
| B. | 根据P=Fv可知,汽车的牵引力一定与速率成反比 | |
| C. | 由P=$\frac{W}{t}$可知,只要知道t时间内做的功,就可求得任一时刻的功率 | |
| D. | 由P=Fv可知,当发动机功率一定时,牵引力与运动速率成反比 |

 如图所示,在直角坐标系xoy的第一象限区域中,有沿y轴正方向的匀强电场,场强的大小为E=kv0.在第二象限有一半径为r=L的圆形区域的匀强磁场,圆形磁场的圆心O坐标为 (-L,L),与坐标轴分别相切于P点和N点,磁场方向垂直纸面向里.在x=3L处垂直于x轴放置一平面荧光屏,与x轴交点为Q.大量的电子以相同的速率v0在纸面内从P点进入圆形磁场,电子的速度方向在与x轴正方向成θ角的范围内,其中沿y轴正方向的电子经过磁场到达N点,速度与x轴正方向成θ角的电子经过磁场到达M点,且M点坐标为(0,1.5L).忽略电子间的相互作用力,不计电子的重力,电子的比荷为$\frac{e}{m}$=$\frac{{v}_{0}}{kL}$.求:
如图所示,在直角坐标系xoy的第一象限区域中,有沿y轴正方向的匀强电场,场强的大小为E=kv0.在第二象限有一半径为r=L的圆形区域的匀强磁场,圆形磁场的圆心O坐标为 (-L,L),与坐标轴分别相切于P点和N点,磁场方向垂直纸面向里.在x=3L处垂直于x轴放置一平面荧光屏,与x轴交点为Q.大量的电子以相同的速率v0在纸面内从P点进入圆形磁场,电子的速度方向在与x轴正方向成θ角的范围内,其中沿y轴正方向的电子经过磁场到达N点,速度与x轴正方向成θ角的电子经过磁场到达M点,且M点坐标为(0,1.5L).忽略电子间的相互作用力,不计电子的重力,电子的比荷为$\frac{e}{m}$=$\frac{{v}_{0}}{kL}$.求: 如图甲所示,A、B两物体与水平面间的动摩擦因数相同,A的质量为3kg.A以一定的初速度向右滑动,与B发生碰撞(碰撞时间极短),碰前A的速度变化如图乙中图线I所示,碰后A、B的速度变化分别如图线Ⅱ、Ⅲ所示,g取10m/s2,求:
如图甲所示,A、B两物体与水平面间的动摩擦因数相同,A的质量为3kg.A以一定的初速度向右滑动,与B发生碰撞(碰撞时间极短),碰前A的速度变化如图乙中图线I所示,碰后A、B的速度变化分别如图线Ⅱ、Ⅲ所示,g取10m/s2,求: