题目内容
17. 如图所示.倾角为θ的固定斜面上有一质量为m的物体.在水平推力F的作用下沿斜面以速度v匀速向上移动了距离S.如果物体与斜面间的动摩擦因数为μ,则( )
如图所示.倾角为θ的固定斜面上有一质量为m的物体.在水平推力F的作用下沿斜面以速度v匀速向上移动了距离S.如果物体与斜面间的动摩擦因数为μ,则( )| A. | 力F所做的功FSsinθ | |
| B. | 斜面体对物体做的功为mgSsinθ-FScosθ | |
| C. | 物体摩擦力所做的功为μ(mgcosθ-Fsinθ)S | |
| D. | 物体的重力做功为mgS |
分析 对m受力分析,由功的公式可求得重力、推力及摩擦力的功;再由动能定理可求得斜面体对物体所做的功;注意斜面体做功包括摩擦力和支持力做功.
解答 解:A、由W=Flcosθ可知B对.力F所做的功W=FScosθ;故A错误;
B、对推动过程由动能定理可知,斜面体对物体所做的功等于重力和推力做功的代数和;故为mgSsinθ-FScosθ;故B正确;
C、由于物体对斜面体的压力为mgcosθ+Fsinθ;故摩擦力所做的功为μ(mgcosθ+Fsinθ)S;故C错误;
D、重力做功W=mgh=-mgssinθ;故D错误;
故选:B.
点评 本题关键是根据恒力做功的表达式求解,要注意力F做功与是否受摩擦力无关;同时注意动能定理的正确应用和功的准确表达.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
7. 如图所示,人造卫星A、B在同一平面内绕地心O做匀速圆周运动.已知A、B连线与A、O连线间的夹角最大为θ,则卫星A、B的角速度之比$\frac{{ω}_{1}}{{ω}_{2}}$等于( )
如图所示,人造卫星A、B在同一平面内绕地心O做匀速圆周运动.已知A、B连线与A、O连线间的夹角最大为θ,则卫星A、B的角速度之比$\frac{{ω}_{1}}{{ω}_{2}}$等于( )
 如图所示,人造卫星A、B在同一平面内绕地心O做匀速圆周运动.已知A、B连线与A、O连线间的夹角最大为θ,则卫星A、B的角速度之比$\frac{{ω}_{1}}{{ω}_{2}}$等于( )
如图所示,人造卫星A、B在同一平面内绕地心O做匀速圆周运动.已知A、B连线与A、O连线间的夹角最大为θ,则卫星A、B的角速度之比$\frac{{ω}_{1}}{{ω}_{2}}$等于( )| A. | sin3θ | B. | $\frac{1}{si{n}^{3}θ}$ | C. | $\sqrt{si{n}^{3}θ}$ | D. | $\sqrt{\frac{1}{si{n}^{3}θ}}$ |
12.关于物体的动量,下列说法正确的是( )
| A. | 物体的动量越大,它的惯性也越大 | |
| B. | 动量是矢量,其方向一定与物体速度的方向相同 | |
| C. | 动量大的物体,它的速度可能大 | |
| D. | 物体的动量越大,它所受的合外力越大 |
2.水的折射率为n,距水面深h处有一个点光源,岸上的人看到水面被该光源照亮的圆形区域的直径为( )
| A. | 2htan(arc sin$\frac{1}{n}$) | B. | 2htan(arc sin n) | C. | 2htan(arc cos$\frac{1}{n}$) | D. | 2hcot(arc cos n) |
6. 如图所示,图a、b、c的圆心均在地球的自转轴线上,对环绕地球做匀速圆周运动而言( )
如图所示,图a、b、c的圆心均在地球的自转轴线上,对环绕地球做匀速圆周运动而言( )
 如图所示,图a、b、c的圆心均在地球的自转轴线上,对环绕地球做匀速圆周运动而言( )
如图所示,图a、b、c的圆心均在地球的自转轴线上,对环绕地球做匀速圆周运动而言( )| A. | 卫星的轨道可能为a | B. | 卫星的轨道可能为b | ||
| C. | 卫星的轨道可能为c | D. | 同步卫星的轨道只可能为b |
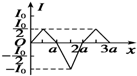
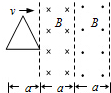 如图所示,一边长为a,电阻为R的等边三角形线框在外力作用下以速度v匀速穿过宽度均为a的两个匀强磁场区域,两磁场磁感应强度的大小均为B,方向相反,线框运动方向与底边平行且与磁场边缘垂直.以逆时针方向为电流正方向,从图示位置开始线框中感应电流I与沿运动方向的位移x的关系图象为( )
如图所示,一边长为a,电阻为R的等边三角形线框在外力作用下以速度v匀速穿过宽度均为a的两个匀强磁场区域,两磁场磁感应强度的大小均为B,方向相反,线框运动方向与底边平行且与磁场边缘垂直.以逆时针方向为电流正方向,从图示位置开始线框中感应电流I与沿运动方向的位移x的关系图象为( )


 如图所示,在直角坐标系xoy的第一象限区域中,有沿y轴正方向的匀强电场,场强的大小为E=kv0.在第二象限有一半径为r=L的圆形区域的匀强磁场,圆形磁场的圆心O坐标为 (-L,L),与坐标轴分别相切于P点和N点,磁场方向垂直纸面向里.在x=3L处垂直于x轴放置一平面荧光屏,与x轴交点为Q.大量的电子以相同的速率v0在纸面内从P点进入圆形磁场,电子的速度方向在与x轴正方向成θ角的范围内,其中沿y轴正方向的电子经过磁场到达N点,速度与x轴正方向成θ角的电子经过磁场到达M点,且M点坐标为(0,1.5L).忽略电子间的相互作用力,不计电子的重力,电子的比荷为$\frac{e}{m}$=$\frac{{v}_{0}}{kL}$.求:
如图所示,在直角坐标系xoy的第一象限区域中,有沿y轴正方向的匀强电场,场强的大小为E=kv0.在第二象限有一半径为r=L的圆形区域的匀强磁场,圆形磁场的圆心O坐标为 (-L,L),与坐标轴分别相切于P点和N点,磁场方向垂直纸面向里.在x=3L处垂直于x轴放置一平面荧光屏,与x轴交点为Q.大量的电子以相同的速率v0在纸面内从P点进入圆形磁场,电子的速度方向在与x轴正方向成θ角的范围内,其中沿y轴正方向的电子经过磁场到达N点,速度与x轴正方向成θ角的电子经过磁场到达M点,且M点坐标为(0,1.5L).忽略电子间的相互作用力,不计电子的重力,电子的比荷为$\frac{e}{m}$=$\frac{{v}_{0}}{kL}$.求: 假设蹦极运动员的质量为M,他身上拴着质量为m,总长为L的弹性绳,弹性绳竖直放置,如图所示,在运动员离开跳台到弹性绳拉直前的这一过程中弹性绳的形变忽略不计,求此过程中蹦极运动员下落y距离时蹦极运动员的速度.
假设蹦极运动员的质量为M,他身上拴着质量为m,总长为L的弹性绳,弹性绳竖直放置,如图所示,在运动员离开跳台到弹性绳拉直前的这一过程中弹性绳的形变忽略不计,求此过程中蹦极运动员下落y距离时蹦极运动员的速度.