��Ŀ����
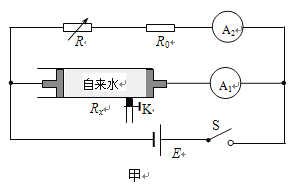
����Ŀ����ͼ��ʾ��ˮƽ���õ�ƽ�а��������ԭ�������岻���磬�ϼ���ӵأ����ļ��峤L=0.1m����������d=0.4cm����һ����ͬ�Ĵ���������ͬ�ij��ٶ��Ⱥ������������ƽ�м������룬�����������������䵽�¼����ϣ��������������ת�Ƶ��¼����Ҿ��ȷֲ����¼����ϡ���ǰһ���䵽�¼�����ʱ��һ�����ܿ�ʼ����������䡣��֪������Ϊm=2��10��6kg�������q=1��10��8C������������ΪC=1��F��ȡg=10m/s2��
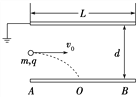
��1��Ϊʹ��һ����ǡ�������¼�����е㵽������Ե��B��֮�ڣ�����������ٶ�v0��ȡֵ��Χ��
��2�����������Ե���1�����г��ٶ�v0��Сֵ���䣬��������ж��ٸ��������䵽�¼����ϣ�
���𰸡���1��2.5m/s��v0��5m/s��2��600��
�������������������1����һ������ƽ���˶���ˮƽ����������ֱ���˶�����ֱ���������������˶������ݸ߶�![]() ��ˮƽλ�ƴ�
��ˮƽλ�ƴ�![]() ��L��������ٶ�
��L��������ٶ�![]() ��ȡֵ��Χ����2�������Ӹպôӱ�Ե�ɳ�ʱ���䵽�¼����ϵĴ�������࣬����ţ�ٵڶ����ɺ��˶�ѧ��ʽ�������ĵ���Q���������������䵽�¼������ӵĸ�����
��ȡֵ��Χ����2�������Ӹպôӱ�Ե�ɳ�ʱ���䵽�¼����ϵĴ�������࣬����ţ�ٵڶ����ɺ��˶�ѧ��ʽ�������ĵ���Q���������������䵽�¼������ӵĸ�����
��1�������Ӵ����¼����е㡢��Ե�ij��ٶȷֱ�Ϊ![]() ����ƫתλ��Ϊ
����ƫתλ��Ϊ![]()
��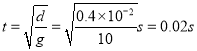
ˮƽ���� ![]()
������ã� ![]()
�����ӵij��ٶ�����2.5m/s��v0��5m/s��
��2�������Ӹպôӱ�Ե�ɳ�ʱ�������ΪQ����ǿΪE������ѹΪU����ţ�ٵڶ����ɵã� ![]()
ƫתλ�ƣ� ![]() ��ˮƽλ�ƣ�
��ˮƽλ�ƣ� ![]() ����
����![]()
������ã� ![]()
��![]() �����
�����![]()
������䵽�¼������ӵĸ���Ϊ�� ![]() ��
��