题目内容
8. 如图所示,物重30N,用OC绳悬挂在O点,OC绳能承受最大拉力为20$\sqrt{3}$N,再用一绳系OC绳的A点,BA绳能承受的最大拉力为30N,现用水平力缓慢的拉绳BA,求:能把OA绳拉到与竖直方向的最大角度.
如图所示,物重30N,用OC绳悬挂在O点,OC绳能承受最大拉力为20$\sqrt{3}$N,再用一绳系OC绳的A点,BA绳能承受的最大拉力为30N,现用水平力缓慢的拉绳BA,求:能把OA绳拉到与竖直方向的最大角度.
分析 在拉动的过程中,为了保证绳不拉断,先判断出那根绳先断,用这根绳刚要断时的拉力做为临界条件分析计算.
解答 解:当OA绳与竖直方向的夹角θ逐渐增大时,OA和BA绳中的拉力都逐渐增大.当其中某一根的拉力达到它本身能承受的最大拉力时,就不能再增大角度了.
结点A的受力如图所示.
由图可知,OA绳的拉力总是大于AB绳的拉力,若OA绳的拉力先达到断裂的临界值,应用OA的承受的最大拉力作为临界条件求解.
此时:
FOA=20$\sqrt{3}$N
FAC=G=30N,
FAB=$\sqrt{{F}_{OA}^{2}-{F}_{AC}^{2}}$=10$\sqrt{3}$N<30N,所以一定是OA绳先断.
此时:cosθ=$\frac{{F}_{AC}}{{F}_{OA}}=\frac{30}{20\sqrt{3}}$=$\frac{\sqrt{3}}{2}$
即:OA偏离竖直方向的最大角度θ=30°
答:能把OA绳拉到与竖直方向的最大角度为30°.
点评 此题是物体受力平衡的应用,解决此类题目需要找出临界状态,再应用受力平衡计算即可.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
18. 一个物体静置于斜面上,当斜面倾角θ缓慢增大时,物体仍静止在斜面上,如图所示.下列对此过程的分析中正确的是( )
一个物体静置于斜面上,当斜面倾角θ缓慢增大时,物体仍静止在斜面上,如图所示.下列对此过程的分析中正确的是( )
 一个物体静置于斜面上,当斜面倾角θ缓慢增大时,物体仍静止在斜面上,如图所示.下列对此过程的分析中正确的是( )
一个物体静置于斜面上,当斜面倾角θ缓慢增大时,物体仍静止在斜面上,如图所示.下列对此过程的分析中正确的是( )| A. | 物体所受重力和支持力的合力逐渐增大 | |
| B. | 物体对斜面的压力逐渐增大 | |
| C. | 物体所受重力和静摩擦力的合力逐渐增大 | |
| D. | 物体所受重力、静摩擦力和支持力的合力保持不变 |
19.某同学在“用打点计时器测速度”的实验中,用打点计时器记录了被小车拖动的纸带的运动情况,在纸带上确定出A、B、C、D、E、F、G共7个计数点.其相邻点间的距离如图1所示,每两个相邻的测量点之间的时间间隔为0.10s.

(1)试根据纸带上各个计数点间的距离,计算出打下B、D两个点时小车的瞬时速度,并将速度值填入表(要求保留3位有效数字)
(2)将B、C、D、E、F各个时刻的瞬时速度标在直角坐标系中,并在图2的坐标系中画出小车的瞬时速度随时间变化的关系图线.
(3)由作出的速度时间关系图线计算小车运动的加速度a=0.80m/s2(保留2位有效数字)

(1)试根据纸带上各个计数点间的距离,计算出打下B、D两个点时小车的瞬时速度,并将速度值填入表(要求保留3位有效数字)
| 速度 | VB | VC | VD | VE | VF |
| 数值(m/s) | 0.400 | 0.479 | 0.560 | 0.640 | 0.721 |
(3)由作出的速度时间关系图线计算小车运动的加速度a=0.80m/s2(保留2位有效数字)
16. 如图所示,QA=3×10-12C,QB=-3×10-12C,A,B相距6cm,在水平方向的外加电场作用下,保持静止,且悬线处于竖直方向,求A,B连线中点处的电场强度的大小.(A,B可视为点电荷)
如图所示,QA=3×10-12C,QB=-3×10-12C,A,B相距6cm,在水平方向的外加电场作用下,保持静止,且悬线处于竖直方向,求A,B连线中点处的电场强度的大小.(A,B可视为点电荷)
 如图所示,QA=3×10-12C,QB=-3×10-12C,A,B相距6cm,在水平方向的外加电场作用下,保持静止,且悬线处于竖直方向,求A,B连线中点处的电场强度的大小.(A,B可视为点电荷)
如图所示,QA=3×10-12C,QB=-3×10-12C,A,B相距6cm,在水平方向的外加电场作用下,保持静止,且悬线处于竖直方向,求A,B连线中点处的电场强度的大小.(A,B可视为点电荷)
13.龟兔赛跑中,兔子和乌龟的位移时间图象如图所示,关于兔子和乌龟的运动,下列说法正确的是( )


| A. | 兔子和乌龟是同时出发的 | |
| B. | 乌龟一直做匀加速直线运动 | |
| C. | 在0~t5时间内,乌龟的平均速度比兔子大 | |
| D. | 兔子在t5时刻发现落后并加速追赶,最终兔子还是先到了预定地点x3 |
20. 长L=0.5m的轻杆,其一端连接着一个零件A,A的质量m=2kg.现让A 在 竖直平面内绕O点做匀速圆周运动,如图所示.在A通过最高点时的速率为1m/s (g=10m/s2),则A对杆的作用力( )
长L=0.5m的轻杆,其一端连接着一个零件A,A的质量m=2kg.现让A 在 竖直平面内绕O点做匀速圆周运动,如图所示.在A通过最高点时的速率为1m/s (g=10m/s2),则A对杆的作用力( )
 长L=0.5m的轻杆,其一端连接着一个零件A,A的质量m=2kg.现让A 在 竖直平面内绕O点做匀速圆周运动,如图所示.在A通过最高点时的速率为1m/s (g=10m/s2),则A对杆的作用力( )
长L=0.5m的轻杆,其一端连接着一个零件A,A的质量m=2kg.现让A 在 竖直平面内绕O点做匀速圆周运动,如图所示.在A通过最高点时的速率为1m/s (g=10m/s2),则A对杆的作用力( )| A. | 4N | B. | 24N | C. | 16N | D. | 44N |
18.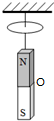 如图所示,一圆形闭合铜环由高处静止开始下落,穿过一根竖直悬挂的条形磁铁,铜环的中心轴线与条形磁铁的中轴线始终保持重合.若取磁铁中心所在位置为O点,则闭合铜环( )
如图所示,一圆形闭合铜环由高处静止开始下落,穿过一根竖直悬挂的条形磁铁,铜环的中心轴线与条形磁铁的中轴线始终保持重合.若取磁铁中心所在位置为O点,则闭合铜环( )
 如图所示,一圆形闭合铜环由高处静止开始下落,穿过一根竖直悬挂的条形磁铁,铜环的中心轴线与条形磁铁的中轴线始终保持重合.若取磁铁中心所在位置为O点,则闭合铜环( )
如图所示,一圆形闭合铜环由高处静止开始下落,穿过一根竖直悬挂的条形磁铁,铜环的中心轴线与条形磁铁的中轴线始终保持重合.若取磁铁中心所在位置为O点,则闭合铜环( )| A. | 在O点处感应电动势最大 | |
| B. | 在O点上方时的安培力方向与O点下方时的安培力方向相同 | |
| C. | 在O点上方时的感应电流方向与在O点下方时的感应电流方向相反 | |
| D. | 在O点上方加速下落,在O点下方减速下落 |

 如图所示,在光滑水平面上竖直固定一半径为R的光滑半圆槽轨道,其底端恰与水平面相切,质量为m的小球以某一初速度经半圆槽轨道最低点B滚上半圆槽,小球恰能通过最高点C后落回到水平面上的A点,求:(不计空气阻力,重力加速度为g)
如图所示,在光滑水平面上竖直固定一半径为R的光滑半圆槽轨道,其底端恰与水平面相切,质量为m的小球以某一初速度经半圆槽轨道最低点B滚上半圆槽,小球恰能通过最高点C后落回到水平面上的A点,求:(不计空气阻力,重力加速度为g)