题目内容
3.某单极发电机的简化原理如图所示.在长直线圈中垂直于线圈对称轴上固定一根半径为r的圆形金属导轨,可自由转动的金属杆CD位于线圈对称轴上,杆上固连一长为r的金属棒OA,可随杆转动,金属棒的另一端与圆形金属导轨接触良好.CD杆右侧固连一圆盘,其半径为$\frac{r}{2}$,并绕有细线,在恒力拉动下,圆盘和杆一起旋转.构成线圈的导线一端通过电刷P连接到杆CD上,另一端连接到圆形金属导轨Q点,回路的等效总电阻为R.线圈放置在磁感应强度为B0的匀强磁场中,方向水平向右.(提示:当线圈中通有电流I时,电流在线圈内产生的磁感应强度大小B=aI,其中a是由线圈决定的常数)
(1)断开开关S,当金属棒转速为ω时,求金属棒OA两端电动势;
(2)闭合开关S,当金属棒以稳定转速ω0转动时,求回路电流强度I;
(3)闭合开关S,当金属棒以稳定转速ω0转动时,不计摩擦阻力,求作用在细线上的恒力大小F.
分析 (1)根据法拉第电磁感应定律,即可求解;
(2)根据闭合电路欧姆定律,结合磁感应强度大小B=αI,即可求解;
(3)根据稳定转动时的Fv=I2R,结合线速度与角速度的关系,即可求解.
解答 解:(1)由法拉第电磁感应定律,则有:E=Brv=$\frac{1}{2}{B}_{0}ω{r}^{2}$
(2)线圈内总磁感应强度:B′=B0+B
而B=αI,
且I=$\frac{E}{R}$=$B′\frac{1}{2R}{ω}_{0}{r}^{2}$
解得:I=$\frac{{B}_{0}{r}^{2}{ω}_{0}}{2R-α{r}^{2}{ω}_{0}}$
应有:${ω}_{0}<\frac{2R}{α{r}^{2}}$
(3)金属棒稳定转动时,则有:Fv=I2R;
而v=$\frac{{ω}_{0}r}{2}$
解得:F=$\frac{2{I}^{2}R}{r{ω}_{0}}$=$(\frac{{B}_{0}{r}^{2}{ω}_{0}}{2R-α{r}^{2}{ω}_{0}})^{2}•\frac{2R}{r{ω}_{0}}$
答:(1)断开开关S,当金属棒转速为ω时,金属棒OA两端电动势为$\frac{1}{2}{B}_{0}ω{r}^{2}$;
(2)闭合开关S,当金属棒以稳定转速ω0转动时,回路电流强度I为$\frac{{B}_{0}{r}^{2}{ω}_{0}}{2R-α{r}^{2}{ω}_{0}}$;
(3)闭合开关S,当金属棒以稳定转速ω0转动时,不计摩擦阻力,作用在细线上的恒力大小F为$(\frac{{B}_{0}{r}^{2}{ω}_{0}}{2R-α{r}^{2}{ω}_{0}})^{2}•\frac{2R}{r{ω}_{0}}$.
点评 考查法拉第电磁感应定律与闭合电路欧姆定律的应用,掌握线速度与角速度的关系,注意金属棒稳定转动时,则有:Fv=I2R,是解题的突破口.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案| A. | 电动势越大的电源,将其他形式的能转化为电能的本领越大 | |
| B. | 电源两极间的电压等于电源电动势 | |
| C. | 电源电动势的数值等于内、外电压之和 | |
| D. | 电源电动势与外电路的组成无关 |
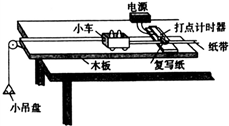 如图为“探究加速度与力、质量关系”的实验装置示意图.
如图为“探究加速度与力、质量关系”的实验装置示意图.(1)实验过程中,以下操作正确的是BC
A.平衡摩擦力时,先调节长木板一端滑轮的高度,使细线与长木板平行,接着将长木板水平放置,让小车连着已经穿过打点计时器的纸带,给打点计时器通电,让小车在小吊盘内的细砂和小吊盘的牵引下运动,从打出的纸带判断小车是否做匀速运动.
B.平衡摩擦力时,先调节长木板一端滑轮的高度,使细线与长木板平行,将长木板的一端垫起适当的高度,让小车连着已经穿过打点计时器的纸带,撤去小吊盘内的细砂和小吊盘,给打点计时器通电,轻推小车,从打出的纸带判断小车是否做匀速运动.
C.每次改变小车的质量时,不需要重新平衡摩擦力
D.实验时,应先放开小车,后接通电源
(2)一组同学在做“加速度a与质量m的关系”实验时,保持小吊盘及盘中砝码的质量一定,改变小车的总质量m,测出相应的加速度,得小车的加速度a与对应的质量m数据如表:
| 实验次数 | 1 | 2 | 3 | 4 | 5 |
| 小车的加速度a/(m•s-2) | 1.25 | 1.00 | 0.80 | 0.50 | 0.40 |
| 小车的总质量m/kg | 0.400 | 0.500 | 0.625 | 1.000 | 1.250 |
| 小车的总质量m的倒数m-1/kg-1 | 2.50 | 2.00 | 1.60 | 1.00 | 0.80 |
(3)建立坐标系在答卷纸上画出图象.
 如图所示,在垂直于纸面的范围足够大的匀强磁场中,有一个10匝的矩形线圈abcd,刚开始线圈平面与磁场垂直,此时线圈内的磁通量为0.05Wb,现线圈以O1O2为轴在0.5s内转动180°,求:
如图所示,在垂直于纸面的范围足够大的匀强磁场中,有一个10匝的矩形线圈abcd,刚开始线圈平面与磁场垂直,此时线圈内的磁通量为0.05Wb,现线圈以O1O2为轴在0.5s内转动180°,求: 如图所示,物重30N,用OC绳悬挂在O点,OC绳能承受最大拉力为20$\sqrt{3}$N,再用一绳系OC绳的A点,BA绳能承受的最大拉力为30N,现用水平力缓慢的拉绳BA,求:能把OA绳拉到与竖直方向的最大角度.
如图所示,物重30N,用OC绳悬挂在O点,OC绳能承受最大拉力为20$\sqrt{3}$N,再用一绳系OC绳的A点,BA绳能承受的最大拉力为30N,现用水平力缓慢的拉绳BA,求:能把OA绳拉到与竖直方向的最大角度.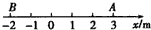 如图所示,一个物体在2s内从A运动到B,初位置的坐标是xA=3m,末位置的坐标xB=-2m,它的坐标变化量△s等于多少?位移是多少?平均速度是多少?
如图所示,一个物体在2s内从A运动到B,初位置的坐标是xA=3m,末位置的坐标xB=-2m,它的坐标变化量△s等于多少?位移是多少?平均速度是多少?