题目内容
3.如图所示,竖直墙壁上固定一轻质弹簧,轻质弹簧水平放置;A点左侧的水平面光滑,右侧水平面粗糙;在A点右侧x=5m远处竖直放置一半圆形圆管轨道,圆管内壁光滑,轨道半径R=0.4m.现将一质量为m=0.1kg的小滑块放在弹簧的右端(不拴接),用力向左推滑块而压缩弹簧,使弹簧具有Ep弹=2J的弹性势能;放手后,小滑块向右弹出.已知小滑块与A点右侧粗糙水平面间的动摩擦因数μ=0.2.取g=10m/s2.
(1)试求小滑块运动到半圆形圆管轨道最低点B处时对轨道的压力.
(2)若改变半圆形圆管轨道的位置(向左或向右平移),可使得被弹出的小滑块到达半圆形圆管轨道最高点C处时对轨道压力的大小等于滑块的重力,试求此时半圆形圆管轨道最低点B与点A之间的距离.
分析 (1)从小滑块被释放到达B点的过程中,据动能定理列式,在B点根据向心力公式列式,而弹力做的功等于弹簧具有的弹性势,联立方程即可求解;
(2)在圆周最高点C处,滑块对轨道的压力等于其重力,包含两种情况:第一,当压力方向向上(滑块受到的支持力向下),第二,当压力方向向下(滑块受到的支持力向上),在C点根据向心力公式列式,整个过程中根据动能定理列式,联立方程即可求解.
解答 解:(1)设放手后弹簧对小滑块做的功为W弹,小滑块克服摩擦力做的功为W;运动到半圆形圆管轨道最低点B处时的速度为vB,受到轨道的支持力为FN.则
W弹=Ep弹…①
W=μmgx …②
由动能定理得:W弹-W=$\frac{1}{2}$mvB2…③
由牛顿第二定律得:FN-mg=m$\frac{{{v_B}^2}}{R}$…④
联立①②③④式,解得:FN=6N
由牛顿第三定律可得,小滑块运动到半圆形圆管轨道最低点B处时对轨道的压力大小为6N,方向向下.
(2)小滑块到达半圆形圆管轨道最高点C处时对轨道压力的大小等于滑块的重力包含两种情形.
第一种情形:小滑块受到圆管轨道向下的压力.设此时小滑块到达半圆形圆管轨道最高点C处时的速度大小为vC1,受到圆管轨道向下的压力为FN1,半圆形圆管轨道最低点B与点A之间的距离为x1.则
FN1=mg…⑤
mg+FN1=m$\frac{{{v_{C1}}^2}}{R}$…⑥
W弹-μmgx1-mg•2R=$\frac{1}{2}$mvC12…⑦
联立⑤⑥⑦式,代入数据解得:x1=4m
第二种情形:小滑块受到圆管轨道向上的支持力.设此时小滑块到达半圆形圆管轨道最高点C处时的速度大小为vC2,受到圆管轨道向上的支持力为FN2,半圆形圆管轨道最低点B与点A之间的距离为x2.则
FN2=mg…⑧
mg-FN2=m$\frac{{{v_{C2}}^2}}{R}$…⑨
W弹-μmgx2-mg•2R=$\frac{1}{2}$mvC22…=10 ⑩
联立⑧⑨=10 ⑩式,代入数据解得:x2=6m
答:(1)滑块运动到半圆形轨道最低点B处时对轨道的压力为6N;
(2)改变半圆形轨道的位置(左右平移),使得被弹出的滑块到达半圆形轨道最高点C处时对轨道的压力大小等于滑块的重力,则AB之间的距离应调整为4m或6m.
点评 本题是动能定理与向心力公式的综合应用来处理圆周运动问题.利用功能关系解题的优点在于不用分析复杂的运动过程,只关心初末状态即可,平时要加强训练深刻体会这一点.

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案| A. | 物体的高度和所受重力 | B. | 物体所受的重力和初速度 | ||
| C. | 物体的高度和初速度 | D. | 物体所受的重力、高度和初速度 |
 如图所示,一列向右传播的简谐波,波速大小为0.6m/s,P质点的横坐标为x=0.96m,从图中状态开始计时,求:
如图所示,一列向右传播的简谐波,波速大小为0.6m/s,P质点的横坐标为x=0.96m,从图中状态开始计时,求:(1)P质点刚开始振动时,振动方向如何?
(2)经过多长时间,P质点第一次达到波谷?
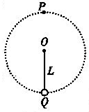 如图所示,长为L的轻杆一端固定一质量为m的小球,另一端有固定轴O,杆可在竖直平面内绕轴O无摩擦转动,已知小球通过最高点P时,速度的大小为vP=$\sqrt{2gl}$,已知小球通过最低点Q时,速度的大小为vQ=$\sqrt{6gl}$,则小球的运动情况为( )
如图所示,长为L的轻杆一端固定一质量为m的小球,另一端有固定轴O,杆可在竖直平面内绕轴O无摩擦转动,已知小球通过最高点P时,速度的大小为vP=$\sqrt{2gl}$,已知小球通过最低点Q时,速度的大小为vQ=$\sqrt{6gl}$,则小球的运动情况为( )| A. | 小球到达圆周轨道的最高点P点受到轻杆向上的弹力 | |
| B. | 小球到达圆周轨道的最低点Q点受到轻杆向上的弹力 | |
| C. | 小球到达圆周轨道的最高点P,且在P点不受轻杆的作用力 | |
| D. | 若小球到达圆周轨道的最高点P速度增大,则P点受到轻杆向下的弹力增大 |
 科技实验小组在清理实验器材时发现在一个精密电阻R上标有“45Ω 5W”字样,于是他将电阻R、标有“3V 0.6W”字样的小灯泡L和电源等器材组成如图所示实验电路,已知电表均为理想电表,则下列推断正确的是( )
科技实验小组在清理实验器材时发现在一个精密电阻R上标有“45Ω 5W”字样,于是他将电阻R、标有“3V 0.6W”字样的小灯泡L和电源等器材组成如图所示实验电路,已知电表均为理想电表,则下列推断正确的是( )| A. | 调整滑动变阻器,当电流表示数小于$\frac{1}{3}$A时,电阻R的阻值小于45Ω | |
| B. | 无论滑动变阻器触头P向右还是向左移动,电阻R消耗的电功率始终保持5W不变 | |
| C. | 调整滑动变阻器,使电压表表示数为12V,小灯泡恰能正常工作 | |
| D. | 若换不同功率的小灯泡与精密电阻R串联,则小灯泡的功率不能超过5W |
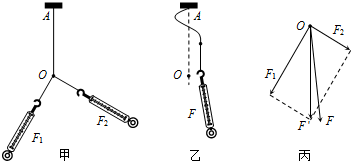


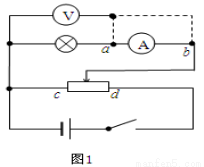
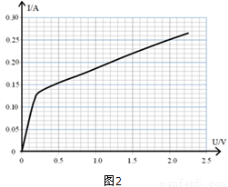
 一磁场宽度为L,磁感应强度为B,如图所示,一电荷质量为m、带电荷量为-q,不计重力,以某一速度(方向如图)射入磁场.若不使其从右边界飞出,则电荷的速度应为多大?
一磁场宽度为L,磁感应强度为B,如图所示,一电荷质量为m、带电荷量为-q,不计重力,以某一速度(方向如图)射入磁场.若不使其从右边界飞出,则电荷的速度应为多大?