题目内容
19. 一磁场宽度为L,磁感应强度为B,如图所示,一电荷质量为m、带电荷量为-q,不计重力,以某一速度(方向如图)射入磁场.若不使其从右边界飞出,则电荷的速度应为多大?
一磁场宽度为L,磁感应强度为B,如图所示,一电荷质量为m、带电荷量为-q,不计重力,以某一速度(方向如图)射入磁场.若不使其从右边界飞出,则电荷的速度应为多大?
分析 粒子在磁场中做匀速圆周运动,粒子恰好不从右边界飞出时,其轨迹与磁场右边界相切,由由几何知识求出粒子的轨道半径,然后由牛顿第二定律求出粒子的速度.
解答 解:若要粒子不从右边界飞出,当达最大速度时运动轨迹如图,
由几何知识可求得半径r,即 r+rcosθ=L,得 r=$\frac{L}{1+cosθ}$
又由牛顿第二定律得 Bqv=$\frac{mv2}{r}$,
所以v=$\frac{Bqr}{m}$=$\frac{BqL}{m(1+cosθ)}$.
故若不使其从右边界飞出,则电荷的速度应为v≤$\frac{BqL}{m(1+cosθ)}$.
答:若不使其从右边界飞出,则电荷的速度应小于等于$\frac{BqL}{m(1+cosθ)}$.
点评 根据题意画出粒子满足要求的轨迹,由几何知识求出粒子的临界半径,然后应用牛顿第二定律即可正确解题.

练习册系列答案
相关题目
8. 如图所示,车厢长度为L,质量为M,静止于光滑的水平面上,车厢内有一质量为m的物体以初速度v0向右运动,与车厢撞n次后静止于车厢中,这时车厢的速度为( )
如图所示,车厢长度为L,质量为M,静止于光滑的水平面上,车厢内有一质量为m的物体以初速度v0向右运动,与车厢撞n次后静止于车厢中,这时车厢的速度为( )
 如图所示,车厢长度为L,质量为M,静止于光滑的水平面上,车厢内有一质量为m的物体以初速度v0向右运动,与车厢撞n次后静止于车厢中,这时车厢的速度为( )
如图所示,车厢长度为L,质量为M,静止于光滑的水平面上,车厢内有一质量为m的物体以初速度v0向右运动,与车厢撞n次后静止于车厢中,这时车厢的速度为( )| A. | 0 | B. | v0 | C. | $\frac{m{v}_{0}}{M+m}$ | D. | $\frac{M{v}_{0}}{M-m}$ |

 如图所示是一个半径为R的轮子,它绕固定转动轴O顺时针方向转动,两侧各有一个长为L的竖直杆MO和NQ,它们都固定在天花板上M、N处(如图所示).两轻杆上距轴为a处各固定一宽度为b的摩擦块(上下厚度不计).摩擦块与轮子间动摩擦因数都是μ(μ<$\frac{a}{b}$),不计杆与摩擦块的重力.为使轮子刹停,在两杆下端P、Q之间用轻绳悬挂一重物.刚好使三根细绳之间夹角都相等.
如图所示是一个半径为R的轮子,它绕固定转动轴O顺时针方向转动,两侧各有一个长为L的竖直杆MO和NQ,它们都固定在天花板上M、N处(如图所示).两轻杆上距轴为a处各固定一宽度为b的摩擦块(上下厚度不计).摩擦块与轮子间动摩擦因数都是μ(μ<$\frac{a}{b}$),不计杆与摩擦块的重力.为使轮子刹停,在两杆下端P、Q之间用轻绳悬挂一重物.刚好使三根细绳之间夹角都相等. 如图所示为一个边长分别为$\sqrt{3}$l和l的矩形区域ABCD,在该区域内有竖直方向的匀强电场时,一个质量为m,带电量为q的粒子沿水平方向以速度v从A点射入该区域,恰好从C点离开电场.(不计重力影响)
如图所示为一个边长分别为$\sqrt{3}$l和l的矩形区域ABCD,在该区域内有竖直方向的匀强电场时,一个质量为m,带电量为q的粒子沿水平方向以速度v从A点射入该区域,恰好从C点离开电场.(不计重力影响) 如图所示,M、N为两块带等量异种电荷的平行金属板,两板间电压可取从零到某一最大值之间的各种数值.静止的带电粒子带电荷量为+q,质量为m(不计重力),从点P经电场加速后,从小孔Q进入N板右侧的匀强磁场区域,磁感应强度大小为B,方向垂直于纸面向外,CD为磁场边界上的一绝缘板,它与N板的夹角为θ=45°,孔Q到板的下端C的距离L,当M、N两板间电压取最大值时,粒子恰垂直打在CD板上,求:
如图所示,M、N为两块带等量异种电荷的平行金属板,两板间电压可取从零到某一最大值之间的各种数值.静止的带电粒子带电荷量为+q,质量为m(不计重力),从点P经电场加速后,从小孔Q进入N板右侧的匀强磁场区域,磁感应强度大小为B,方向垂直于纸面向外,CD为磁场边界上的一绝缘板,它与N板的夹角为θ=45°,孔Q到板的下端C的距离L,当M、N两板间电压取最大值时,粒子恰垂直打在CD板上,求: 如图所示的平面直角坐标系中存在有界的场区,y轴左侧有沿x轴正向的匀强电场E=1×105N/C,第一象限内有沿y轴负向大小也为E=1×105N/C的匀强电场,第四象限-L<y<0的区域内有一垂直于纸面向里的匀强磁场B=1T.今在A(-a,a)点将一个质量为m=8×10-25kg(重力不计),电量为q=+1.6×10-19C的点电荷由静止释放,已知a=1m.求:
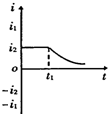
如图所示的平面直角坐标系中存在有界的场区,y轴左侧有沿x轴正向的匀强电场E=1×105N/C,第一象限内有沿y轴负向大小也为E=1×105N/C的匀强电场,第四象限-L<y<0的区域内有一垂直于纸面向里的匀强磁场B=1T.今在A(-a,a)点将一个质量为m=8×10-25kg(重力不计),电量为q=+1.6×10-19C的点电荷由静止释放,已知a=1m.求: 如图所示,S闭合后,流过线圈L的电流恒为i1,流过灯泡A的电流恒为i2,且i1>>i2.在t1时刻将S迅速断开,在较短一段时间内流过灯泡的电流随时间变化的图象是( )
如图所示,S闭合后,流过线圈L的电流恒为i1,流过灯泡A的电流恒为i2,且i1>>i2.在t1时刻将S迅速断开,在较短一段时间内流过灯泡的电流随时间变化的图象是( )