题目内容
如图所示,  和
和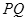 为固定在绝缘水平面上两平行光滑金属导轨,导轨左端
为固定在绝缘水平面上两平行光滑金属导轨,导轨左端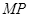 间接有阻值为
间接有阻值为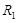 =
=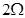 导线;导轨右端接有与水平轨道相切、半径
导线;导轨右端接有与水平轨道相切、半径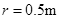 内壁光滑的半圆金属轨道。导轨间距
内壁光滑的半圆金属轨道。导轨间距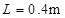 ,电阻不计。导轨所在平面
,电阻不计。导轨所在平面 区域内有竖直向上
区域内有竖直向上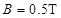 的匀强磁场。导轨上长度也为
的匀强磁场。导轨上长度也为 、质量
、质量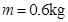 、电阻
、电阻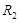 =
=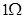 的金属棒
的金属棒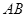 以
以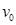 =
=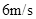 速度进入磁场区域,离开磁场区域后恰好能到达半圆轨道的最高点,运动中金属棒始终与导轨保持良好接触。已知重力加速度
速度进入磁场区域,离开磁场区域后恰好能到达半圆轨道的最高点,运动中金属棒始终与导轨保持良好接触。已知重力加速度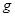 =
=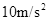 。求:
。求: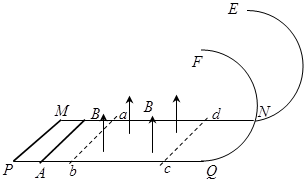
(1)金属棒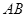 刚滑出磁场右边界
刚滑出磁场右边界 时的速度
时的速度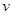 的大小;
的大小;
(2)金属棒滑过磁场区的过程中,导线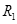 中产生的热量
中产生的热量 。
。
(1)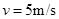 (2)
(2)
解析试题分析:(1)在轨道的最高点,根据牛顿定律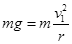 ①
①
金属棒刚滑出磁场到最高点,根据机械能守恒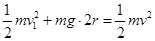 ②
②
由①②式代入数据解得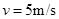 ③
③
(2)对金属棒滑过磁场的过程中,根据能量关系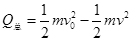 ④
④
对闭合回路,根据热量关系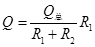 ⑤
⑤
由④⑤式并代入数据得 ⑥
⑥
考点:牛顿定律、机械能守恒定律及能量守恒定律。

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
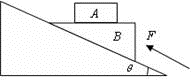
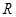 .A点与圆心O等高,B、C点处于竖直直径的两端.PA是一段绝缘的竖直圆管,两者在A点平滑连接,整个装置处于方向水平向右的匀强电场中.一质量为
.A点与圆心O等高,B、C点处于竖直直径的两端.PA是一段绝缘的竖直圆管,两者在A点平滑连接,整个装置处于方向水平向右的匀强电场中.一质量为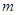 、电荷量为
、电荷量为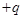 的小球从管内与C点等高处由静止释放,一段时间后小球离开圆管进入圆弧轨道运动.已知匀强电场的电场强度
的小球从管内与C点等高处由静止释放,一段时间后小球离开圆管进入圆弧轨道运动.已知匀强电场的电场强度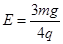 (
(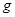 为重力加速度),小球运动过程中的电荷量保持不变,忽略圆管和轨道的摩擦阻力.求:
为重力加速度),小球运动过程中的电荷量保持不变,忽略圆管和轨道的摩擦阻力.求: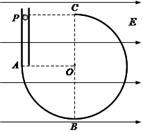
 和滑块到斜面顶端的距离
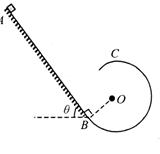
和滑块到斜面顶端的距离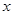 的关系如图2所示。斜面倾角为37°,长为L。有一半径
的关系如图2所示。斜面倾角为37°,长为L。有一半径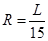 的光滑竖直半圆轨道刚好与斜面底端B相接,且直径BC与水平面垂直,假设滑块经过B点时没有能量损失。当滑块运动到斜面底端B又与质量为m的静止小球(可视为质点)发生弹性碰撞(已知:
的光滑竖直半圆轨道刚好与斜面底端B相接,且直径BC与水平面垂直,假设滑块经过B点时没有能量损失。当滑块运动到斜面底端B又与质量为m的静止小球(可视为质点)发生弹性碰撞(已知: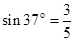 ,
,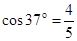 )。求:
)。求: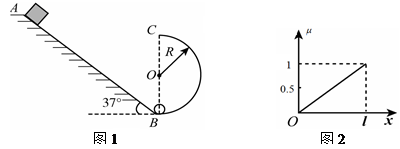
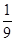 ×10-6C,如图所示,将小球B缓缓拉离竖直位置,当绳与竖直方向的夹角为60°时,将其由静止释放,小球B将在竖直面内做圆周运动.已知释放瞬间绳刚好张紧,但无张力.静电力常量
×10-6C,如图所示,将小球B缓缓拉离竖直位置,当绳与竖直方向的夹角为60°时,将其由静止释放,小球B将在竖直面内做圆周运动.已知释放瞬间绳刚好张紧,但无张力.静电力常量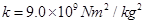 ,g取10m/s2。求
,g取10m/s2。求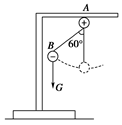

 m/s.试计算:(g取10m/s2)
m/s.试计算:(g取10m/s2)
