题目内容
13.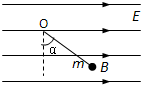 一条长为l的细线上端固定在O点,下端系一个质量为m的带电小球,将它置于一个很大的匀强电场中,电场强度为E,方向水平向右,已知小球在B点时平衡,细线与竖直线的夹角为α,求:
一条长为l的细线上端固定在O点,下端系一个质量为m的带电小球,将它置于一个很大的匀强电场中,电场强度为E,方向水平向右,已知小球在B点时平衡,细线与竖直线的夹角为α,求:(1)当悬线与竖直方向的夹角为多大时,才能使小球由静止释放后,细线到竖直位置时,小球的速度恰好为零.
(2)当细线与竖直方向成α角时,至少要给小球一个多大的冲量,才能使小球做圆周运动?
分析 (1)根据小球在B点静止,由平衡条件求出电场力大小.小球由静止释放后运动至最低点过程,根据动能定理求解释放时悬线与竖直方向的夹角.
(2)当小球运动到关于B对称的A点时,恰好由重力和电场力的合力提供向心力时,小球能做完整的圆周运动,根据牛顿第二定律求出临界速度,再由动能定理求出小球的初速度,再由冲量和动量关系确定.
解答 解:(1)小球静止在B点时,根据平衡条件得
qE=mgtanα
设从θ释放,释放点到最低点过程,根据动能定理得
mgL(1-cosθ)-FLsinθ=0
得到:sinθtanα+cosθ=1,tanα=$\frac{1}{sinθ}-\frac{cosθ}{sinθ}=tg\frac{θ}{2}$,
解得:θ=2α,
(2)设当小球运动到关于B对称的A点时,临界速度为vA.根据牛顿第二定律得
$\sqrt{(Eq)^{2}+(mg)^{2}}$=$m\frac{{v}_{A}^{2}}{L}$
解得:${v}_{A}^{2}=gL\sqrt{1+tg{α}^{2}}$
由A到B过程,根据动能定理得
mg2Lcosα+Eq2Lsinα=$\frac{1}{2}m{v}_{B}^{2}-\frac{1}{2}m{v}_{A}^{2}$
解得:vB=$\sqrt{\frac{4gL}{cosα}+gL\sqrt{1+tg{α}^{2}}}$,
给小球的冲量:I=mvB=m$\sqrt{\frac{4gL}{cosα}+gL\sqrt{1+tg{α}^{2}}}$,
答:(1)当悬线与竖直方向的夹角为2α,才能使小球由静止释放后,细线到竖直位置时,小球的速度恰好为零.
(2)当细线与竖直方向成α角时,至少要给小球一个m$\sqrt{\frac{4gL}{cosα}+gL\sqrt{1+tg{α}^{2}}}$的冲量,才能使小球做圆周运动.
点评 本题是带电粒子在电场和重力场的复合场中运动问题,分析受力情况是基础.对于第(2)问找到类似于竖直平面内圆周运动最高点的条件是关键.

| A. | 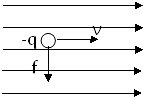 | B. | 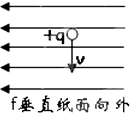 | C. | 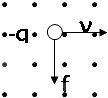 | D. | 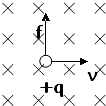 |
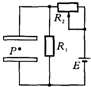 如图所示,在水平放置的平行板电容器之间,有一带电油滴P处于静止状态,油滴所带的电荷保持不变,现在要使该油滴向下运动,可采取下列哪些措施( )
如图所示,在水平放置的平行板电容器之间,有一带电油滴P处于静止状态,油滴所带的电荷保持不变,现在要使该油滴向下运动,可采取下列哪些措施( )| A. | 其他条件不变,使电容器两极板缓慢靠近 | |
| B. | 其他条件不变,使电容器两极板缓慢远离 | |
| C. | 其他条件不变,将变阻器的滑片缓慢向左移动 | |
| D. | 其他条件不变,将变阻器的滑片缓慢向右移动 |
A、把打点计时器固定在桌子上 B、安好纸带
C、松开纸带让物体带着纸带运动 D、接通低压交流电源
E、取下纸带 F、断开开关
这些步骤正确的排列顺序为ABDCEF.
(2)用打点计时器记录了被小车拖动的纸带的运动情况,在纸带上确定出A、B、C、D、E、F、G共7个计数点.其相邻点间的距离如图所示,每两个相邻的计数点之间还有4个打印点未画出.

①试根据纸带上各个计数点间的距离,计算出打下B、C、D、E、F五个点时小车的瞬时速度,并将各个速度值填入表(要求保留3位有效数字)
| vB | vC | vD | vE | vF | |
| 数值 (m/s) | 0.400 | 0.479 | 0.560 | 0.640 | 0.721 |
③由所画速度-时间图象求出小车加速度为0.80m/s2(该空保留两位有效数字)
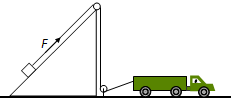 如图所示,一辆卡车后的拉绳通过定滑轮用力F拉位于粗糙斜面上重为G的木箱,使之沿斜面加速向上移动.在移动过程中,木箱受到斜面的摩擦力为Ff.下列说法正确的是( )
如图所示,一辆卡车后的拉绳通过定滑轮用力F拉位于粗糙斜面上重为G的木箱,使之沿斜面加速向上移动.在移动过程中,木箱受到斜面的摩擦力为Ff.下列说法正确的是( )| A. | F对木箱做的功等于木箱增加的动能 | |
| B. | 木箱克服重力做的功等于木箱增加的重力势能 | |
| C. | F、G和Ff对木箱做的功代数和等于木箱增加的动能 | |
| D. | F和Ff对木箱做的功代数和等于木箱增加的机械能 |
 一电阻额定功率为0.01W,阻值不详.用欧姆表粗测其阻值约为40kΩ(阻值随温度的变化可以忽略).现有下列实验器材,请选择合适的器材,并设计恰当的电路,以便较准确地测定其阻值.
一电阻额定功率为0.01W,阻值不详.用欧姆表粗测其阻值约为40kΩ(阻值随温度的变化可以忽略).现有下列实验器材,请选择合适的器材,并设计恰当的电路,以便较准确地测定其阻值.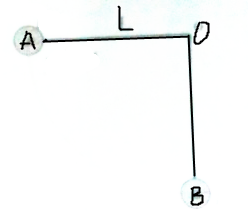 如图,大小相同两个小球挂在同一水平点,线长L且相等,A球质量mA=5$\sqrt{10}$m,B球质量mB=m,现将A球拉至水平,释放后使之与B球正碰,B球恰好能上升到最高点,
如图,大小相同两个小球挂在同一水平点,线长L且相等,A球质量mA=5$\sqrt{10}$m,B球质量mB=m,现将A球拉至水平,释放后使之与B球正碰,B球恰好能上升到最高点,
 如图,一身高H=1.8m的人走近一圆柱型容器前,他发现容器中装满了某种透明的液体,当他离容器还有0.8m时,他沿靠近他的上方容器壁方向观察恰好看见容器的远离他那一端的底角处,他量得容器的深h=1.2m,直径为0.9m.
如图,一身高H=1.8m的人走近一圆柱型容器前,他发现容器中装满了某种透明的液体,当他离容器还有0.8m时,他沿靠近他的上方容器壁方向观察恰好看见容器的远离他那一端的底角处,他量得容器的深h=1.2m,直径为0.9m.