题目内容
在光滑的水平轨道上有两个半径都是r的小球A和B，质量分别是为m和2m.当两球心的距离大于l(l比2r大得多)时，两球之间无相互作用力;当两球心间的距离等于或小于l时，两球之间存在相互作用的恒定斥力F.设A球从远离B球处以速度v0沿两球心连线向原来静止的B球运动,如图3-10-22所示.欲使两球不发生接触，v0必须满足什么条件?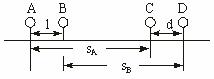
解析:当球心距离小于l后，A球受到斥力而做匀减速直线运动，B球受到斥力而做初速度为零的匀加速运动.当两球的速度相等时两球间的距离达到最小.即
vA=vB.
不相撞的条件就是两球间的最小距离要大于2r,如图所示.设A球的位移为sA，B球的位移为sB，两球不接触的条件是两球心间的距离应满足
d=sB+l-sA＞2r
由牛顿第二定律得两球加速度分别为
aA=
,aB=
由运动公式知，两球末速度分别为
vA=v0-aAt,vB=aBt
由运动学公式知，两球位移分别为
sA=v0t-
aAt2
sB=
aBt2
联立以上各式解得v0＜
.
答案:v0＜
练习册系列答案
中考解读考点精练系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
（2011?江门一模）在光滑的水平轨道上有质量为m的物体A，处于静止状态，物体B的质量也为m，由不可伸长的轻绳悬挂于O点，B与轨道接触但不挤压．某时刻开始受到水平方向的恒力F的作用，经过的距离为L时撤掉F，A再运动一段距离后与物体B碰撞，求：
（2006?红桥区模拟）在光滑的水平轨道上有两个半径都是r的小球A和B，质量分别为m和2m，当两球心间的距离大于L（L比2r大得多）时，两球之间无相互作用力；当两球心间的距离等于或小于L时，两球之间存在相互作用的恒定斥力F．设A球从远离B球处以速度v0沿球连心线向原来静止的B球运动，如图所示．欲使两球不发生接触，v0必须满足什么条件？
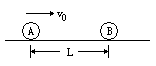
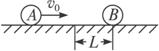
相互作用的恒定斥力F,现A球从远离B球处以速度V0沿两球心连接向原来静止的B球运动，欲时两球不发生接触，V0必须满足的条件？