题目内容
 (2011?江门一模)在光滑的水平轨道上有质量为m的物体A,处于静止状态,物体B的质量也为m,由不可伸长的轻绳悬挂于O点,B与轨道接触但不挤压.某时刻开始受到水平方向的恒力F的作用,经过的距离为L时撤掉F,A再运动一段距离后与物体B碰撞,求:
(2011?江门一模)在光滑的水平轨道上有质量为m的物体A,处于静止状态,物体B的质量也为m,由不可伸长的轻绳悬挂于O点,B与轨道接触但不挤压.某时刻开始受到水平方向的恒力F的作用,经过的距离为L时撤掉F,A再运动一段距离后与物体B碰撞,求:(1)撤掉F时A的速度?F的作用时间?
(2)若A、B发生完全弹性碰撞,绳长为r,则B在碰后的瞬间轻绳受到的拉力?
(3)若A、B发生的碰撞情况是所有可能发生的碰撞情况中的一种,那么绳长满足什么条件才能使B总能完成完整的圆周运动?
分析:(1)对A由牛顿第二定律定律求的物体的加速度的大小,再由运动学公式即可求得A的速度和F的作用时间;
(2)由动量守恒可以求得B的速度大小,再由向心力的公式可以求得轻绳受到的拉力;
(3)当B的速度最小时,如果B也能够做圆周运动,那么B就总能完成完整的圆周运动,B在最高点时,速度最小应该是恰好只有重力作为向心力的时候.
(2)由动量守恒可以求得B的速度大小,再由向心力的公式可以求得轻绳受到的拉力;
(3)当B的速度最小时,如果B也能够做圆周运动,那么B就总能完成完整的圆周运动,B在最高点时,速度最小应该是恰好只有重力作为向心力的时候.
解答:解:(1)设撤掉F时A的速度为V,经历时间为t,则
由牛顿第二定律及匀变速直线运动规律得:
F=ma ①
L=
②
L=
t ③
由①、②得 V=
⑤
由①、②、③得 t=
⑥
(2)设A与B碰后速度分别为VA,VB,B在碰后瞬间轻绳受到的拉力为T,
由动量守恒定律有:mv=mvA+mvB ⑦
mv2=
m
+
m
⑧
由牛顿第二定律:T-mg=m
⑨
由⑤、⑦、⑧、⑨得:T=mg+
. ⑩
(3)若使B能做完整圆周运动,设运动到最高点时速度为V1,
由牛顿第二定律有:mg=m
(11)
B物体从最低点运动至最高点过程中机械能守恒有:
mVB2=mg2R+
m V12 (12)
由(11)(12)得:VB=
(13)
A碰B后,B获得最小速度为VB′,由动量守恒得:mv=(m+m)VB′(14)
由⑤(14)得:VB′=
(15)
由(13)(15)得:最小半径为Rmin=
(16)
答:(1)撤掉F时A的速度是
,F的作用时间是
.
(2)若A、B发生完全弹性碰撞,绳长为r,则B在碰后的瞬间轻绳受到的拉力是mg+
.
(3)要使B总能完成完整的圆周运动,绳长最小为
.
由牛顿第二定律及匀变速直线运动规律得:
F=ma ①
L=
| v2 |
| 2a |
L=
| v |
| 2 |
由①、②得 V=
|
由①、②、③得 t=
|
(2)设A与B碰后速度分别为VA,VB,B在碰后瞬间轻绳受到的拉力为T,
由动量守恒定律有:mv=mvA+mvB ⑦
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 A |
| 1 |
| 2 |
| v | 2 B |
由牛顿第二定律:T-mg=m
| ||
| r |
由⑤、⑦、⑧、⑨得:T=mg+
| 2FL |
| r |
(3)若使B能做完整圆周运动,设运动到最高点时速度为V1,
由牛顿第二定律有:mg=m
| ||
| R |
B物体从最低点运动至最高点过程中机械能守恒有:
| 1 |
| 2 |
| 1 |
| 2 |
由(11)(12)得:VB=
| 5gR |
A碰B后,B获得最小速度为VB′,由动量守恒得:mv=(m+m)VB′(14)
由⑤(14)得:VB′=
| 1 |
| 2 |
|
由(13)(15)得:最小半径为Rmin=
| FL |
| 10mg |
答:(1)撤掉F时A的速度是
|
|
(2)若A、B发生完全弹性碰撞,绳长为r,则B在碰后的瞬间轻绳受到的拉力是mg+
| 2FL |
| r |
(3)要使B总能完成完整的圆周运动,绳长最小为
| FL |
| 10mg |
点评:本题考查了牛顿第二定律、匀变速直线运动的规律、动量守恒还有匀速圆周运动的知识,本题要注意的是要使B总能完成完整的圆周运动,那么B在最高点时,速度最小应该是恰好只有重力作为向心力的时候.

练习册系列答案
相关题目
 (2011?江门一模)足球运动员在射门时经常让球在前进时旋转,从而绕过前方的障碍物,这就是所谓的“香蕉球”,其轨迹在水平面上的投影如图,下列说法正确的是( )
(2011?江门一模)足球运动员在射门时经常让球在前进时旋转,从而绕过前方的障碍物,这就是所谓的“香蕉球”,其轨迹在水平面上的投影如图,下列说法正确的是( )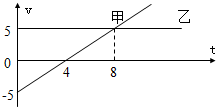 (2011?江门一模)甲、乙两物体在做直线运动,t=0时刻它们从同一地点出发,v-t图象如图,下列说法正确的是( )
(2011?江门一模)甲、乙两物体在做直线运动,t=0时刻它们从同一地点出发,v-t图象如图,下列说法正确的是( ) (2011?江门一模)某理想变压器的原线圈有1400匝,副线圈有700匝并接有负载电阻R,如图所示.当变压器工作时,原、副线圈中( )
(2011?江门一模)某理想变压器的原线圈有1400匝,副线圈有700匝并接有负载电阻R,如图所示.当变压器工作时,原、副线圈中( )