题目内容
1．
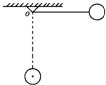一轻绳一端固定在O点，另一端拴一小球，拉起小球使轻绳水平，然后无初速释放小球．如图所示，小球从开始运动至轻绳达竖直位置的过程中，小球重力的瞬时功率的变化情况是（ ）| A． | 一直增大 | B． | 一直减小 | C． | 先增大，后减小 | D． | 先减小，后增大 |
分析 因为重力做功的功率等于重力与速度以及重力与速度方向夹角余弦的乘积，抓住初末位置重力做功的功率大小，判断重力瞬时功率的变化．
解答 解：小球在初位置重力做功的功率为零，在B点，由于重力的方向与速度方向垂直，则重力做功的功率为零，因为初末位置都为零，则A到B过程中重力做功的功率先增大后减小．
故选：C．
点评 解决本题的关键掌握瞬时功率的表达式P=Fvcosθ，知道瞬时功率与平均功率的区别．
练习册系列答案
相关题目
12．地球上的物体，由于地球自转，也随之做匀速圆周运动．那么关于物体的角速度、线速度的大小，以下说法正确的是（ ）
| A． | 北京和南京的角速度大小不相等 | B． | 在两极上的物体线速度最大 | ||
| C． | 赤道上的物体角速度最大 | D． | 在赤道上的物体线速度最大 |
9．2003年2月1日美国哥伦比亚号航天飞机在返回途中解体，造成人类航天史上又一悲剧．若哥伦比亚号航天飞机是在赤道上空飞行，轨道半径为r，飞行方向与地球的自转方向相同．设地球的自转角速度为ω0，地球半径为R，地球表面重力加速度为g，在某时刻航天飞机通过赤道上某建筑物的上方，则到它下次通过该建筑上方所需时间为（ ）
| A． | $\frac{2π}{\sqrt{\frac{g{R}^{2}}{{r}^{3}}-{ω}_{0}}}$ | B． | 2π（$\sqrt{\frac{r^3}{{g{R^2}}}}$+$\frac{1}{ω_0}$） | C． | 2π$\sqrt{\frac{r^3}{{g{R^2}}}}$ | D． | $\frac{2π}{\sqrt{\frac{g{R}^{2}}{{r}^{3}}+{ω}_{0}}}$ |
16．
发射地球同步卫星要经过三个阶段：先将卫星发射至近地圆轨道1，然后使其沿椭圆轨道2运行，最后将卫星送入同步圆轨道3．轨道1、2相切于Q点，轨道2、3相切于P点，如图所示．当卫星分别在轨道1、2、3上正常运行时，则以下说法正确的是（ ）
发射地球同步卫星要经过三个阶段：先将卫星发射至近地圆轨道1，然后使其沿椭圆轨道2运行，最后将卫星送入同步圆轨道3．轨道1、2相切于Q点，轨道2、3相切于P点，如图所示．当卫星分别在轨道1、2、3上正常运行时，则以下说法正确的是（ ）| A． | 卫星在轨道3上的运行速率可能大于7.9km/s | |
| B． | 卫星在轨道3上的速率大于它在轨道1上的速率 | |
| C． | 卫星在轨道2上的运行周期大于它在轨道3上的运行周期 | |
| D． | 卫星分别沿轨道1和轨道2经过Q点时的加速度相等 |
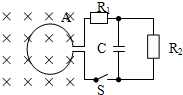截面积为0.2m2的100匝圆形线圈A处在匀强磁场中，磁场方向垂直线圈平面向里，如图所示，磁感应强度正按$\frac{△B}{△t}$=0.02T/s的规律均匀减小，开始时S未闭合．R1=4Ω，R2=6Ω，C=30?F，线圈内阻不计．求：
13．
如图所示，在“研究平抛物体运动”的实验中，用一张印有小方格的纸记录轨迹，小方格的边长l=10cm．若小球在平抛运动途中的几个位置如图中的a、b、c、d所示，则小球平抛的初速度的为v0=（ ）m/s．
如图所示，在“研究平抛物体运动”的实验中，用一张印有小方格的纸记录轨迹，小方格的边长l=10cm．若小球在平抛运动途中的几个位置如图中的a、b、c、d所示，则小球平抛的初速度的为v0=（ ）m/s．| A． | 2m/s | B． | 20m/s | C． | 0.2m/s | D． | 1m/s |
摩托车跨越表演是一项惊险刺激的运动，受到许多极限运动爱好者的喜爱．假设在一次跨越河流的表演中，摩托车离开平台时的速度为24m/s，成功落到对面的平台上，测得两岸平台高度差为5m，如图所示．若飞越中不计空气阻力，摩托车可以近似看成质点，g取10m/s2，求：
光滑的半圆形竖直轨道，其圆心与墙在同一竖直平面内，轨道的下端与水平相切，水平面高出地面H=2R，如图所示，一小球沿水平方向进入半圆形轨道下端，小球沿轨道运动的过程中对轨道的压力的大小和小球与圆心的连线同竖直方向的夹角θ满足关系式F=k+kcosθ，其中k为常数，求：