题目内容
9.2003年2月1日美国哥伦比亚号航天飞机在返回途中解体,造成人类航天史上又一悲剧.若哥伦比亚号航天飞机是在赤道上空飞行,轨道半径为r,飞行方向与地球的自转方向相同.设地球的自转角速度为ω0,地球半径为R,地球表面重力加速度为g,在某时刻航天飞机通过赤道上某建筑物的上方,则到它下次通过该建筑上方所需时间为( )| A. | $\frac{2π}{\sqrt{\frac{g{R}^{2}}{{r}^{3}}-{ω}_{0}}}$ | B. | 2π($\sqrt{\frac{r^3}{{g{R^2}}}}$+$\frac{1}{ω_0}$) | C. | 2π$\sqrt{\frac{r^3}{{g{R^2}}}}$ | D. | $\frac{2π}{\sqrt{\frac{g{R}^{2}}{{r}^{3}}+{ω}_{0}}}$ |
分析 根据人造卫星的万有引力等于向心力,列式求出角速度的表达式,卫星再次经过某建筑物的上空,比地球多转动一圈.
解答 解:人造卫星绕地球做匀速圆周运动,根据万有引力提供向心力,设卫星的质量为m、轨道半径为r、地球质量为M,有:
F=F向
F=$\frac{GMm}{{r}^{2}}$=mω2r
解得
ω=$\sqrt{\frac{GM}{{r}^{3}}}$①
卫星再次经过某建筑物的上空,卫星多转动一圈,有:
(ω-ω0)t=2π ②
地球表面的重力加速度为:g=$\frac{GM}{{R}^{2}}$ ③
联立①②③后,解得:
t=$\frac{2π}{{\sqrt{\frac{{gR}^{2}}{{r}^{3}}}-ω}_{0}}$
故选:A.
点评 本题关键:(1)根据万有引力提供向心力求解出角速度;(2)根据地球表面重力等于万有引力得到重力加速度表达式;(3)根据多转动一圈后再次到达某建筑物上空列式.

练习册系列答案
相关题目
19.如图所示为一正弦式电流通过一电子元件后的波形图,则下列说法正确的是( )


| A. | 这是一种交变电流 | |
| B. | 电流的变化周期是0.02s | |
| C. | 电流的有效值是1A | |
| D. | 电流通过100Ω的电阻时,1s内产生热量为100J |
14.图中,人造地球卫星围绕地球运动,它运行的轨道可能是( )


| A. | ① | B. | ② | C. | ③ | D. | 都有可能 |
1.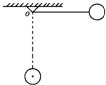 一轻绳一端固定在O点,另一端拴一小球,拉起小球使轻绳水平,然后无初速释放小球.如图所示,小球从开始运动至轻绳达竖直位置的过程中,小球重力的瞬时功率的变化情况是( )
一轻绳一端固定在O点,另一端拴一小球,拉起小球使轻绳水平,然后无初速释放小球.如图所示,小球从开始运动至轻绳达竖直位置的过程中,小球重力的瞬时功率的变化情况是( )
 一轻绳一端固定在O点,另一端拴一小球,拉起小球使轻绳水平,然后无初速释放小球.如图所示,小球从开始运动至轻绳达竖直位置的过程中,小球重力的瞬时功率的变化情况是( )
一轻绳一端固定在O点,另一端拴一小球,拉起小球使轻绳水平,然后无初速释放小球.如图所示,小球从开始运动至轻绳达竖直位置的过程中,小球重力的瞬时功率的变化情况是( )| A. | 一直增大 | B. | 一直减小 | C. | 先增大,后减小 | D. | 先减小,后增大 |
19.以下说法正确的是( )
| A. | 金刚石、食盐、玻璃和水晶都是晶体 | |
| B. | 飘浮在热菜汤表面上的油滴,从上面的观察是圆形的,是因为油滴液体呈各向同性的缘故 | |
| C. | 对于一定量的理想气体,外界对气体做功,气体内能可能减少 | |
| D. | 扩散运动就是布朗运动 |
 如图所示,为一小球做平抛运动的闪光照相照片的一部分,图中背景方格的边长均为5cm,如果取g=10m/s2,那么:
如图所示,为一小球做平抛运动的闪光照相照片的一部分,图中背景方格的边长均为5cm,如果取g=10m/s2,那么: 如图所示,一绳系一球在光滑的桌面上做匀速圆周运动,绳长L=0.1m,当角速度为ω=20rad/s时,绳断开,试分析绳断开后:
如图所示,一绳系一球在光滑的桌面上做匀速圆周运动,绳长L=0.1m,当角速度为ω=20rad/s时,绳断开,试分析绳断开后:
 如图甲所示,一个边长为L的正方形线框固定在匀强磁场(图中未画出)中,磁感应强度的方向垂直于导线框所在平面.规定向里为磁感应强度的正方向,向右为导线框ab边所受安培力的正方向.已知在0~4s时间内导线框ab边所受的安培力如图乙所示,则下图中不能正确表示磁感应强度B随时间变化的图象是( )
如图甲所示,一个边长为L的正方形线框固定在匀强磁场(图中未画出)中,磁感应强度的方向垂直于导线框所在平面.规定向里为磁感应强度的正方向,向右为导线框ab边所受安培力的正方向.已知在0~4s时间内导线框ab边所受的安培力如图乙所示,则下图中不能正确表示磁感应强度B随时间变化的图象是( )


