题目内容
如图所示，固定在竖直平面半径为R的光滑圆环，有质量为m的小球在轨道内侧作圆周运动，小球恰好能通过圆环的最高点．已知重力加速度为g，则小球在运动过程（ ）分析：小球恰好能通过圆环的最高点，轨道对小球没有作用力，由重力提供向心力．根据机械守恒定律可求出小球通过最低点时球的线速度大小．
解答：解：A、由题：小球恰好能通过圆环的最高点，则在最高点时，小球对圆环的压力为零．故A错误．
B、小球恰好能通过圆环的最高点时，由重力提供向心力．故B正确．
C、设小球的质量为m，经过最低点时速度大小为V，则根据机械能守恒定律得
mg?2R+
mv2=
mV2①
又小球在最高点时 mg=m
②
联立上式得 V=
故C错误．
D、小球在圆环内的运动过程中只有重力做功，机械能守恒．故D正确．
故选BD
B、小球恰好能通过圆环的最高点时，由重力提供向心力．故B正确．
C、设小球的质量为m，经过最低点时速度大小为V，则根据机械能守恒定律得
mg?2R+
| 1 |
| 2 |
| 1 |
| 2 |
又小球在最高点时 mg=m
| v2 |
| R |
联立上式得 V=
| 5gR |
D、小球在圆环内的运动过程中只有重力做功，机械能守恒．故D正确．
故选BD
点评：本题考查向心力与机械能守恒定律结合分析问题的能力．对于小球在光滑圆轨道内侧运动到最高点的临界速度与细绳拴的小球模型相同为
．
| gr |
练习册系列答案
名校课堂系列答案
相关题目
如图所示，固定在竖直平板且不可伸长的绝缘轻绳栓一质量为m、电量为q的小球（可视为点电荷），小球平衡时与固定在平板的点电荷Q的连线恰好水平．若小球的质量变为2m时，而其位置仍要保持不变，则小球的电量应该变为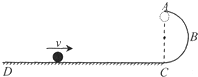
计，g取10m/s2．
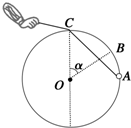如图所示，固定在竖直平面内的半径为R=0.5m的光滑圆环的最高点C处有一个光滑的小孔，一质量为m=0.1kg的小球套在圆环上，一根细线的一端拴着这个小球，细线的另一端穿过小孔C，手拉细线使小球从A处沿圆环向上移动．在下列两种情况下，当小球通过B处，即∠COB=α=740时，求这两种情况下，细线对小球的拉力F的大小和圆环对小球的弹力FN的大小．（不计空气阻力，g取10m/s2；sin37°=0.6，cos37°=0.8；可能用到